最长回文字符串（动态规划） 自用笔记

解题思路:

 动态规划

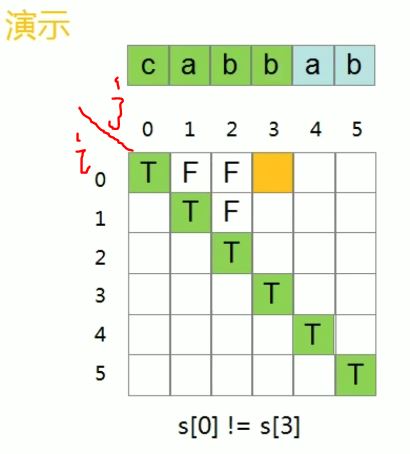
注意事项:

如图所示，dp[0][3]的意思是cabb，不是指c和b。

以对角线为分割，从左往右一列一列的填

参考代码:

#include<iostream>
#include<iomanip>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include <vector>
using namespace std;
int Max(string s);
int main() {                //主函数
    string s;
    while (cin >> s)
    {
        cout<<Max(s)<<endl; //把Max()单独拿出来写
    }
    return 0;
}
int Max(string s) //自定义函数
{
    int len = s.size();
    int maxlen = 1, begin = 0;
    vector<vector<bool>> dp(len, vector<bool>(len, false)); //表示dp[][]矩阵
    for (int i = 0; i < len; i++)  
    {
        dp[i][i] = true;       //主对角线，即字符串单个字符都为回文
    }
    for (int j = 1; j < len; j++) //按列循环，看上方的图理解
    {
        for (int i = 0; i < j; i++)
        {
            if (s[i] == s[j])
            {
                dp[i][j] = (dp[i + 1][j - 1] || (j - i < 3));//当j-i>3时，判断dp[i+1][j-1]是否为true，重复循环;当j-i<3时(类似aba、bb),dp[i][j]=true                                                          //当j-i<3时(类似aba、bb),dp[i][j]=true
            }
        }
    }
    for (int i = 0; i < len; i++)  //此循环是为记录最长回文字符串的长度，单独拿出方便理解
    {
        for (int j = i+1; j < len; j++) //对角线不需要看，所以从j=i+1开始遍历(遍历范围是上三角)
        {
            if (dp[i][j] && j - i + 1 > maxlen)//矩阵中的i和j都是从0开始的，而maxlen初始值设为1，所以j-i>maxlen-1是才更新数据
            {
                maxlen = j - i + 1;
                begin = i;
            }
        }
    }
    return maxlen;
}

参考视频：https://www.bilibili.com/video/BV1f34y1q7vh?from=search&seid=1044414271913720398&spm_id_from=333.337.0.0