python-01背包

解题思路:

①建立一个存放物品的n*2大小的数组commodities[n+1][2]，commodities[i][0]表示第i个物品的重量，commodities[i][1]表示第i个物品的价值。

②建立一个大小为m+1的数组dp[m+1]，dp[i]表示背包剩余容量为m时，所能装载的最大价值。

③状态转移方程为dp[j] = max(dp[j],dp[j-commodities[i][0]]+commodities[i][1])

拿例题来进行测试，每个表格中的数据表示的是dp[i]，即背包容量为i时的最大价值，每扫描一个商品都会对dp数组进行更新。

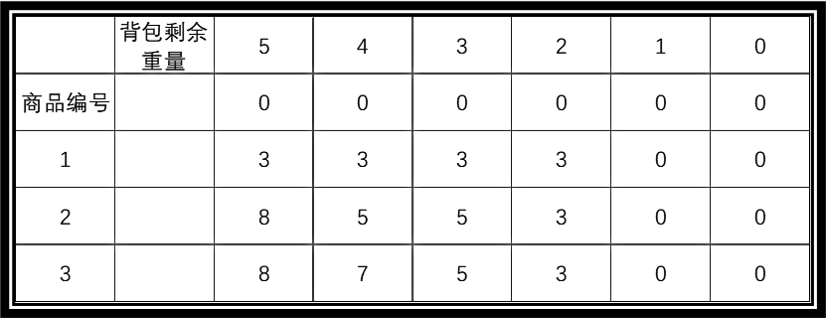
注意事项:

参考代码1:

def f(n,m):  
    commodities = [[0 for j in range(2)] for i in range(n+1)]   
    for i in range(1,n+1):  
        commodities[i][0],commodities[i][1] = map(int,input().strip().split())  
      
    dp = [0 for i in range(m+1)]  
    for i in range(1,n+1):       #对每一个商品进行装载测试
        for j in range(m,commodities[i][0]-1,-1):  #这里j的范围为[m,commodities[i][0]],解决了背包剩下空间不够装该物品的情况
            dp[j] = max(dp[j],dp[j-commodities[i][0]]+commodities[i][1])  
      
    print(dp[m])  
  
  
if __name__ == '__main__':  
    n,m = map(int,input().strip().split())  
    f(n,m)

参考代码2：

dp[i][j]表示有前i种物品，背包容量为j时所能装载的最大价值

def f(n,m):
    dp = [[0 for j in range(m+1)] for i in range(n+1)]
    w = [0 for i in range(n+1)]  #存放物品重量
    v = [0 for i in range(n+1)]  #存放物品价值
    for i in range(1,n+1):
        w[i],v[i] = map(int,input().strip().split())
    for i in range(1,n+1):
        for j in range(m+1):
            if j < w[i]:    #容量不够装第i种物品
                dp[i][j] = dp[i-1][j]
            else:           
                dp[i][j] = max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]) #在装与不装第i种物品间选择价值最大的情况
    print(dp[n][m])
    
                    
if __name__ == '__main__':
    n,m = map(int,input().strip().split())
    f(n,m)