解题思路:
从题目描述看来,两个字符串直接需要通过增、删、改三个操作来变成相同的字符串。那么我们可以发现,只有当两个字符串长度不同时,才需要进行增删操作(第一个字符串比第二个字符串短时进行增操作,反之则进行删操作)只需要将第一个字符串通过增或者删操作变得和第二个字符串等长,那么增或删的字符个数就是答案的一部分,也是必不可少或者无需优化的一部分。所以这一题的关键是改操作,我们得知道两个字符串中,公共的子序列最长的长度,那么剩下的就是我们需要改的长度,所以这一题涉及到最大公共子序列的应用。
最长公共子序列
1.基本概念
首先需要科普一下,最长公共子序列(longest common sequence)和最长公共子串(longest common substring)不是一回事儿。什么是子序列呢?即一个给定的序列的子序列,就是将给定序列中零个或多个元素去掉之后得到的结果。什么是子串呢?给定串中任意个连续的字符组成的子序列称为该串的子串。给一个图再解释一下:
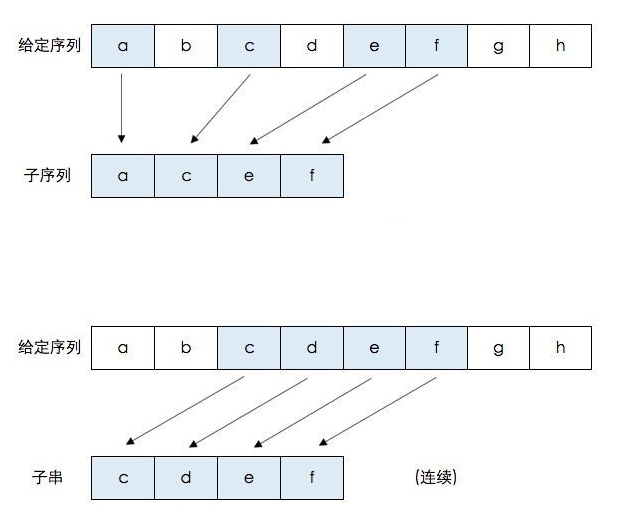
如上图,给定的字符序列: {a,b,c,d,e,f,g,h},它的子序列示例: {a,c,e,f} 即元素b,d,g,h被去掉后,保持原有的元素序列所得到的结果就是子序列。同理,{a,h},{c,d,e}等都是它的子序列。
它的字串示例:{c,d,e,f} 即连续元素c,d,e,f组成的串是给定序列的字串。同理,{a,b,c,d},{g,h}等都是它的字串。
这个问题说明白后,最长公共子序列(以下都简称LCS)就很好理解了。
给定序列s1={1,3,4,5,6,7,7,8},s2={3,5,7,4,8,6,7,8,2},s1和s2的相同子序列,且该子序列的长度最长,即是LCS。
s1和s2的其中一个最长公共子序列是 {3,4,6,7,8}
2.动态规划
求解LCS问题,不能使用暴力搜索方法。一个长度为n的序列拥有 2的n次方个子序列,它的时间复杂度是指数阶,太恐怖了。解决LCS问题,需要借助动态规划的思想。
动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。
3.特征分析
解决LCS问题,需要把原问题分解成若干个子问题,所以需要刻画LCS的特征。
设A=“a0,a1,…,am”,B=“b0,b1,…,bn”,且Z=“z0,z1,…,zk”为它们的最长公共子序列。不难证明有以下性质:
如果am=bn,则zk=am=bn,且“z0,z1,…,z(k-1)”是“a0,a1,…,a(m-1)”和“b0,b1,…,b(n-1)”的一个最长公共子序列;
如果am!=bn,则若zk!=am,蕴涵“z0,z1,…,zk”是“a0,a1,…,a(m-1)”和“b0,b1,…,bn”的一个最长公共子序列;
如果am!=bn,则若zk!=bn,蕴涵“z0,z1,…,zk”是“a0,a1,…,am”和“b0,b1,…,b(n-1)”的一个最长公共子序列。
有些同学,一看性质就容易晕菜,所以我给出一个图来让这些同学理解一下:
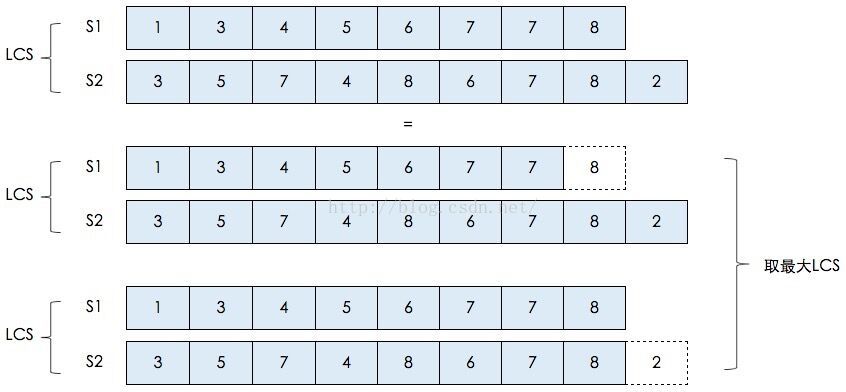
以我在第1小节举的例子(S1={1,3,4,5,6,7,7,8}和S2={3,5,7,4,8,6,7,8,2}),并结合上图来说:
假如S1的最后一个元素 与 S2的最后一个元素相等,那么S1和S2的LCS就等于 {S1减去最后一个元素} 与 {S2减去最后一个元素} 的 LCS 再加上 S1和S2相等的最后一个元素。
假如S1的最后一个元素 与 S2的最后一个元素不等(本例子就是属于这种情况),那么S1和S2的LCS就等于 : {S1减去最后一个元素} 与 S2 的LCS, {S2减去最后一个元素} 与 S1 的LCS 中的最大的那个序列。
4.递归公式
第3节说了LCS的特征,我们可以发现,假设我需要求 a1 ... am 和 b1 .. b(n-1)的LCS 和 a1 ... a(m-1) 和 b1 .. bn的LCS,一定会递归地并且重复地把如a1... a(m-1) 与 b1 ... b(n-1) 的 LCS 计算几次。所以我们需要一个数据结构来记录中间结果,避免重复计算。
假设我们用c[i,j]表示Xi 和 Yj 的LCS的长度(直接保存最长公共子序列的中间结果不现实,需要先借助LCS的长度)。其中X = {x1 ... xm},Y ={y1...yn},Xi = {x1 ... xi},Yj={y1... yj}。可得递归公式如下:
![1642592479241376.png 6X)GEB6]0)O5)C6UOAQZZRG.png](/assets/addons/ueditor/php/upload/image/20220119/1642592479241376.png)
5.计算LCS的长度
这里我不打算贴出相应的代码,只想把这个过程说明白。还是以s1={1,3,4,5,6,7,7,8},s2={3,5,7,4,8,6,7,8,2}为例。我们借用《算法导论》中的推导图:
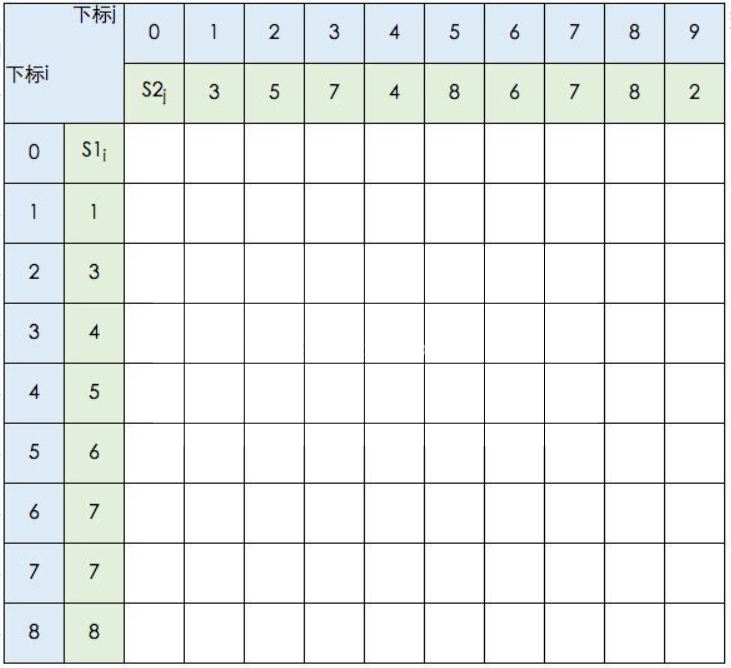
图中的空白格子需要填上相应的数字(这个数字就是c[i,j]的定义,记录的LCS的长度值)。填的规则依据递归公式,简单来说:如果横竖(i,j)对应的两个元素相等,该格子的值 = c[i-1,j-1] + 1。如果不等,取c[i-1,j] 和 c[i,j-1]的最大值。首先初始化该表:
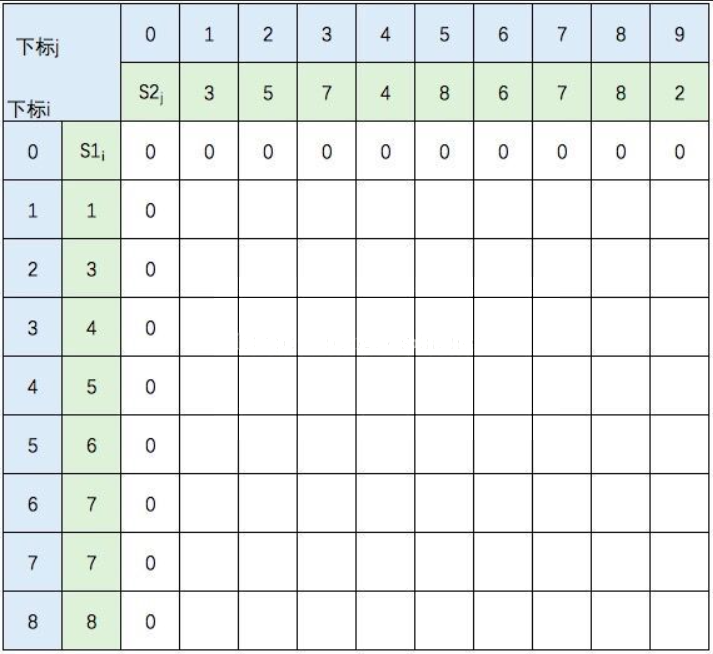
然后,一行一行地从上往下填:
![1642592952179474.png 1ZQFPGUVJI7BS]%O3B3RDRJ.png](/assets/addons/ueditor/php/upload/image/20220119/1642592952179474.png)
S1的元素3 与 S2的元素3 相等,所以 c[2,1] = c[1,0] + 1。继续填充:
![1642593079453726.png 0EAPI5@94WS]Z1ZF2JJW1OU.png](/assets/addons/ueditor/php/upload/image/20220119/1642593079453726.png)
S1的元素3 与 S2的元素5 不等,c[2,2] =max(c[1,2],c[2,1]),图中c[1,2] 和 c[2,1] 背景色为浅黄色。
继续填充:
![1642593170965637.png 1IVK16J84)]W$R)_LB`4_~B.png](/assets/addons/ueditor/php/upload/image/20220119/1642593170965637.png)
![1642593252519158.png WN9G73WHD1{27Y@8IK]RSH4.png](/assets/addons/ueditor/php/upload/image/20220119/1642593252519158.png)
中间几行填写规则不变,直接跳到最后一行:
![1642593312662026.png C7KT_MM]SSHA7$J(92PQGX6.png](/assets/addons/ueditor/php/upload/image/20220119/1642593312662026.png)
至此,该表填完。根据性质,c[8,9] = S1 和 S2 的 LCS的长度,即为5。
6.构造LCS
本文S1和S2的最LCS并不是只有1个,本文并不是着重讲输出两个序列的所有LCS,只是介绍如何通过上表,输出其中一个LCS。
我们根据递归公式构建了上表,我们将从最后一个元素c[8][9]倒推出S1和S2的LCS。
c[8][9] = 5,且S1[8] != S2[9],所以倒推回去,c[8][9]的值来源于c[8][8]的值(因为c[8][8] > c[7][9])。
c[8][8] = 5, 且S1[8] = S2[8], 所以倒推回去,c[8][8]的值来源于 c[7][7]。
以此类推,如果遇到S1[i] != S2[j] ,且c[i-1][j] = c[i][j-1] 这种存在分支的情况,这里请都选择一个方向(之后遇到这样的情况,也选择相同的方向)。
第一种结果为:
![1642593505821305.png H}4T}]]FZ1]`{P6~81LO3`N.png](/assets/addons/ueditor/php/upload/image/20220119/1642593505821305.png)
这就是倒推回去的路径,棕色方格为相等元素,即LCS = {3,4,6,7,8},这是其中一个结果。
如果如果遇到S1[i] != S2[j] ,且c[i-1][j] = c[i][j-1] 这种存在分支的情况,选择另一个方向,会得到另一个结果。
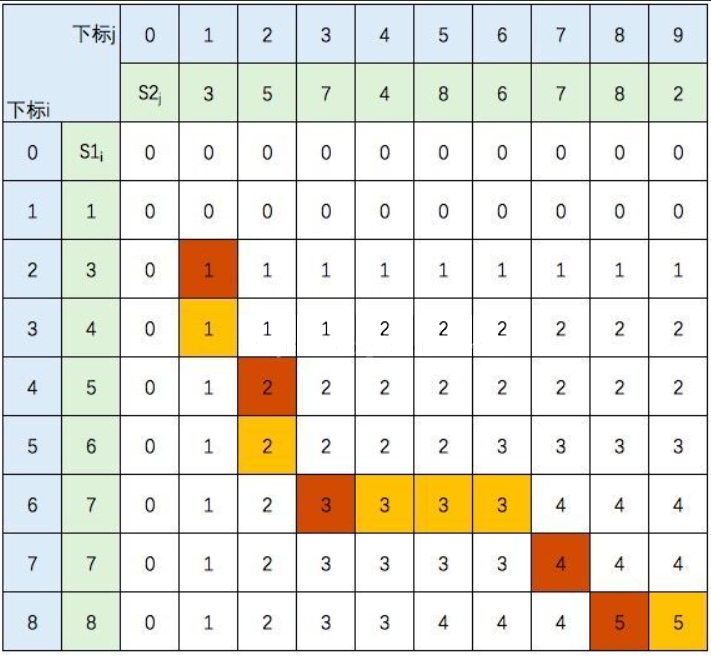
即LCS ={3,5,7,7,8}。
至此就是所有对于最长公共子序列的讲解,虽然比较复杂,但也能直观地表达出这种算法的具体步骤。
参考代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int dp[200][200];
int main()
{
string s1;
string s2;
cin>>s1>>s2;
for(int i=1;i<=s1.length();i++)
for(int j=1;j<=s2.length();j++)
{
if(s1[i-1]==s2[j-1]) dp[i][j]=dp[i-1][j-1]+1;
else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
cout<<max(s1.length(),s2.length())-dp[s1.length()][s2.length()];
return 0;
}0.0分
24 人评分
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程

发表评论 取消回复