战场的数目 （C语言）可以说是基本上纯数学

解题思路:我的C实在是不行，打了好久才过的，我用的基本上是纯数学方法，因为题目给的周长范围最大为10的9次方，所以O(N)的复杂度应该是过不了的，得用O（logN）来写，写一个快速幂，这个代码细节很多，我试错试了好几次，改这些细节比写这些代码时间还长，废话不多说，说思路：

设周长=2i，首先应该得到一个递推公式， f[i] = 3f[i−1]−f[i−2]+（i-2），我是找规律找出来的，但不推荐找规律，我看下面的那位大哥的题解思路很强，我给他复制粘贴一下，这一块其实挺难想的，但到这里才是刚开始。

[左侧或右侧有一个1，那么把这个1删去，对应的方案数f[i−1]
左侧和右侧都有一个1, 删去两次，对应的方案数为f[i−2]
每一列都大于1，把最下面一层删去，对应的方案为f[i−1]
得到公式 f[i] = 3f[i−1]−f[i−2]
最后再减去矩形的方案为 （n / 2 −1）]

这一段是某位大哥的思路。

接下来我的做法应该和他不一样，根据这个递推公式f[i+2] = 3f[i+1]−f[i]+i(i是半周长),通过特征根+待定系数法，得到f[n]的通项公式：

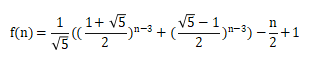
其中n是周长（注意上面的i和这里的n不是一个）

n肯定是偶数，所以n-3是奇数，所以设（1+根5）/2的（n-3）次方=（A+B根5）/2，则（根5-1）/2的（n-3）次方=（B根5-A）/2，他们一相加再除以根5，就只剩B了，所以我们要求的就是B。所以我们用一个数组A[2]来存A和B，然后用快速幂求最终的A和B。我觉得我的这段代码应该是比较好懂的。

但是但是，特别要注意的是你会发现我在快速幂那一段代码全部是模的2X（X=987654321），这是因为奇偶性的问题，我们发现

（（A+B根5）/2）*（（C+D根5）/2）=（E+F根5）/2

如果A和B同奇偶，C和D同奇偶，那么E和F同奇偶，这个展开即证，而且A和B初始值都是1，是同奇偶的，所以A和B永远同奇偶，但是问题是，

模完987654321后，就不一定同奇偶了，因为987654321这是一个奇数（重点），比如说进行一次操作后A=C+2X(C<X)，B=D+X(D<X)那么模987654321后A减去一个偶数，而B减去一个奇数，就不同奇偶了，所以要模2X，在最后的最后再模X。（我一开始没注意到，发现跑着跑着不同奇偶了）

另一个亲身经历，觉得需要注意的点就是，小心运算中某个数会爆掉，虽然我们用的long long，但是X=987654321是个九位数，而long long 的最大值是一个十九位数，X平方再乘个数就会爆掉（心酸），我当时想要不要写个大数运算，但我不会也很麻烦，后来发现我这个程序里最容易爆掉的一行是这里

temp[0]=(((a[0]*a[0]+a[1]*a[1])/2)%(2*X)+2*((a[1]*a[1])%(2*X)))%(2*X);

这是改之后的，一开始我的代码是这样的

temp[0]=((a[0]*a[0]+5*a[1]*a[1])/2)%(2*X);

发现5*a[1]*a[1]这个东西特别容易爆，a[1]最大是2*987654321-1，约等于2*（10的9次方），平方之后乘5就会到2*（10的20次方），会爆，所以我选择把这个乘5分开来写，2*a[1]*a[1]这个东西很接近极限范围，但不会爆，所以我改成了上面的那个写法。

那下面来看一下代码好咯。

注意事项:
注释掉的几行可以看一下运行过程
参考代码:

#include <stdio.h>

#include <stdlib.h>

const X=987654321;

long long A[2];

void f0(long long a[2]){

A[0]=1;

A[1]=1;

}

long long f1(long long a[2]){

long long temp[2];

temp[0]=(((a[0]*a[0]+a[1]*a[1])/2)%(2*X)+2*((a[1]*a[1])%(2*X)))%(2*X);

temp[1]=(a[0]*a[1])%(2*X);

a[0]=temp[0],a[1]=temp[1];

//printf("%lld %lld\n",a[0],a[1]);

}

long long f2(long long a[2]){

long long temp[2];

temp[0]=((a[0]+5*a[1])/2)%(2*X);

temp[1]=((a[0]+a[1])/2)%(2*X);

a[0]=temp[0],a[1]=temp[1];

//printf("%lld %lld\n",a[0],a[1]);

}

int f3(int n){

int m=0;

while(n){

    n>>=1;

    m++;

}

return m;

}

int main()

{

    long long sum;

    int n;

    while((scanf("%d", &n)) != EOF && n != 0){

        if(n<8||n%2==1)printf("0\n");

        else{

            f0(A);

            int m=n-3;

            int p=f3(m)-1;

            int x=1;//这里的x没用，只是用来看运行过程

            while(p>=1){

            if (m&(1<<(p-1))){f1(A);f2(A);x=2*x+1;

            //printf("%d\n",x);

            }

            else {f1(A);x*=2;

            //printf("%d\n",x);

            }

            p--;

            }

            sum=(A[1]-n/2+1+2*X)%X;

            printf("%lld\n",sum);

        }

    }

    return 0;

}