格子刷油漆c++dp(最详细)

看了好多大佬的代码，使用人数最多也是最容易的解法还是动态规划

对于一个1列格子，从左上角第一个顶点出发的路径数为1:

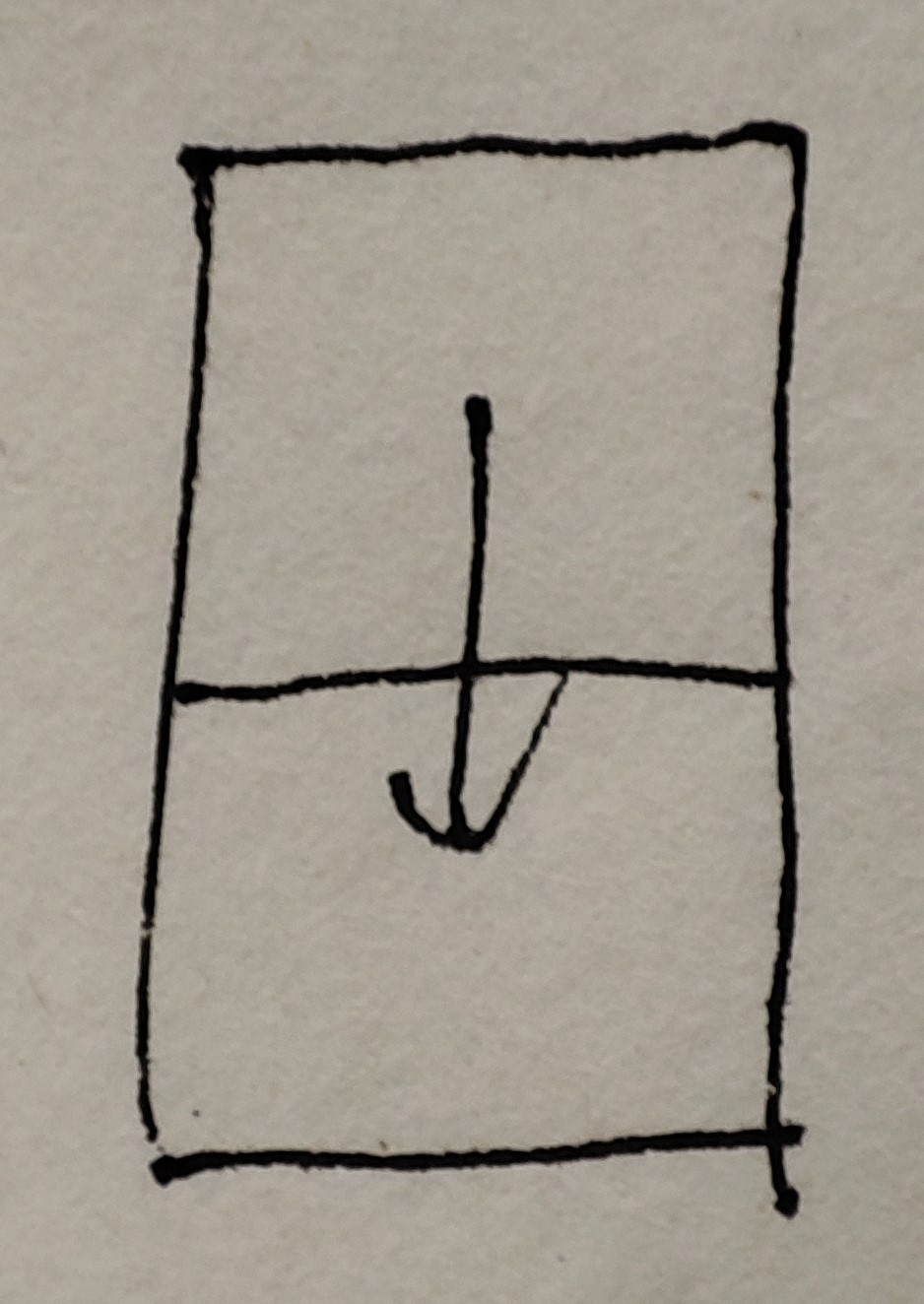
当n=2时，从左上角第一个顶点出发的路径数为6:

那n=3呢？

画出n=3时的表格，我们不难发现n=3与n=2时两者路径数的联系：我们假设在n=2时从左上角第一个格子出发回到第一个格子下方的路径数为b，此时b=2

分别为：

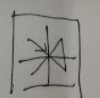
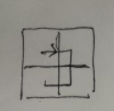
当n=3时从左上角第一个格子出发，可以被划分为两种情况，分别为  左上角第一个格子—>第二列格子 我们注意到此时又分为三种情况：

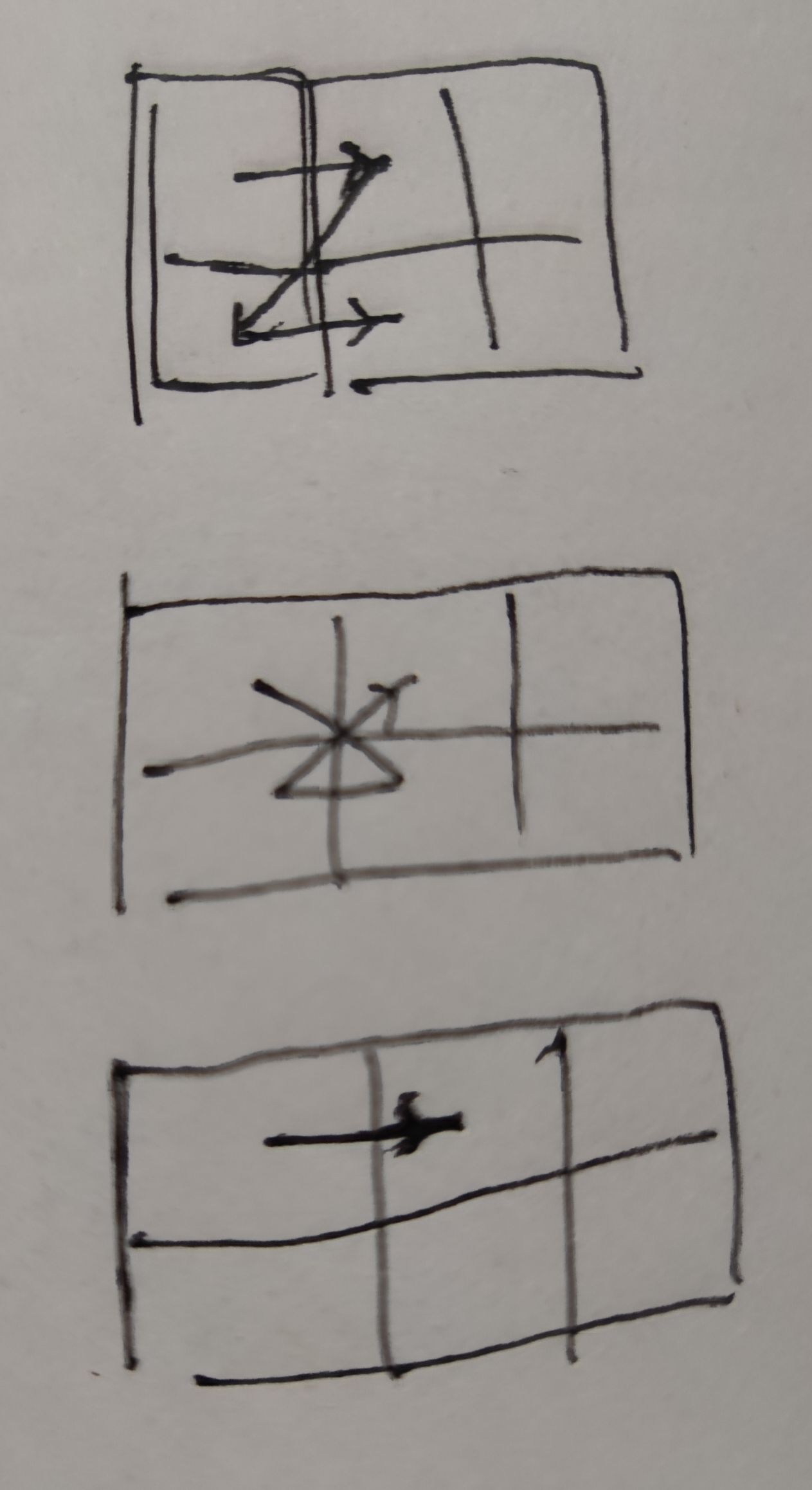
1.对于上图中第一种情况，此时路径数a为n=1时的路径数的两倍(从第三列第一行出发和从第三列第二行出发)

2.对于上图中第二种情况，此时路径数依然为n=1时路径数的两倍

3.对于上图中第三种情况，此时我们应该向第三列移动，最终回到第二列第二行，即a=2*b=4(由于从第一列第二行移动到第二列有两种走法：右移、右下角移动)

第二种情况： 左上角第一个格子—>左下角第一个格子 此时路径数刚好为n=2时的路径数的两倍，如图：

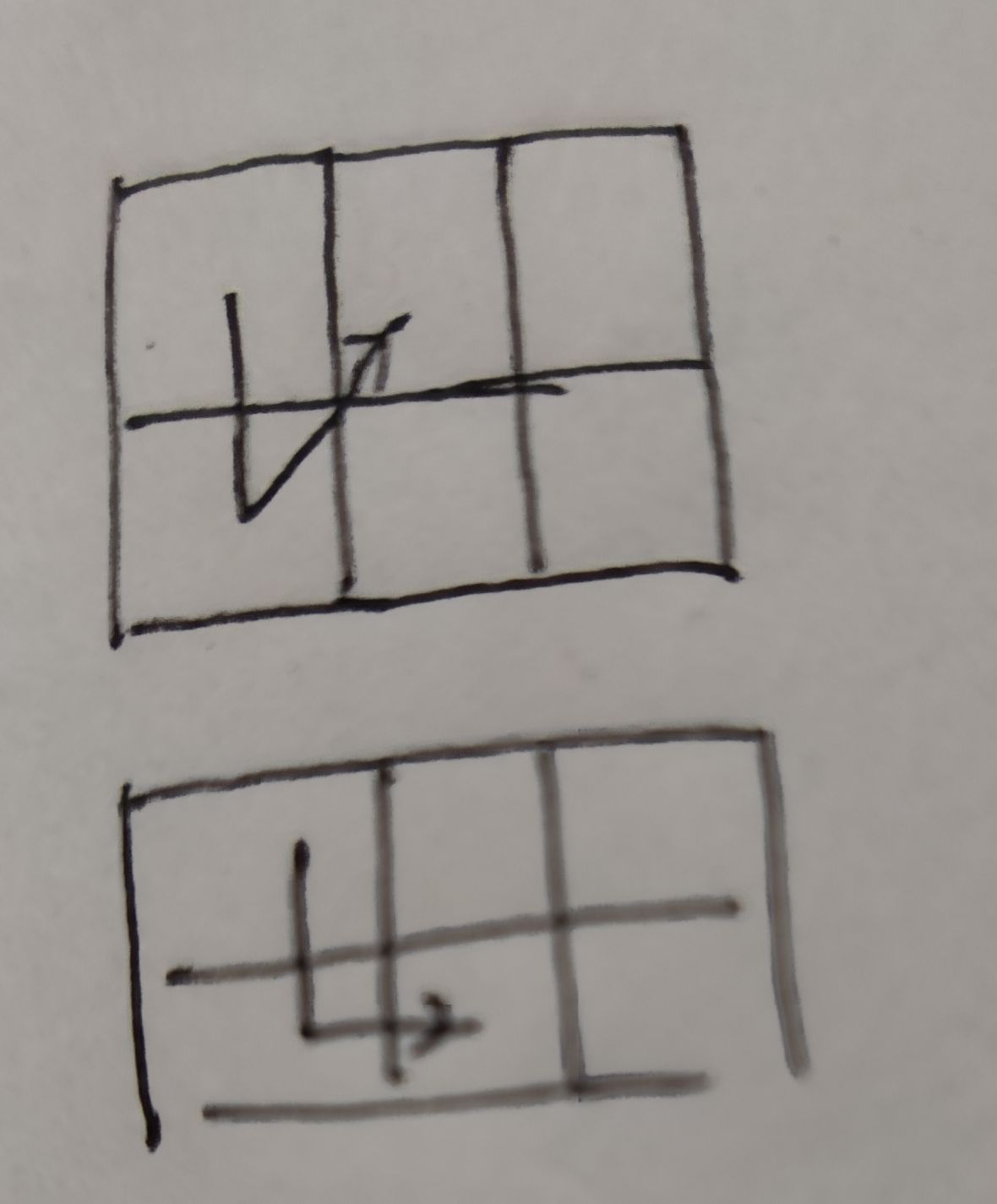
不难看出我们需要定义一个数列来表达从第一列出发回到第一列的路径数b  以及从第一列出发的所有路径数a

我们还发现b[3]=2b[2] (因为从第一列出发最终回到第一列相当于从第一列出发到达第二列，又从第二列出发回到第二列，而第一列到第二列的方法有两种)

因此我们得到关系

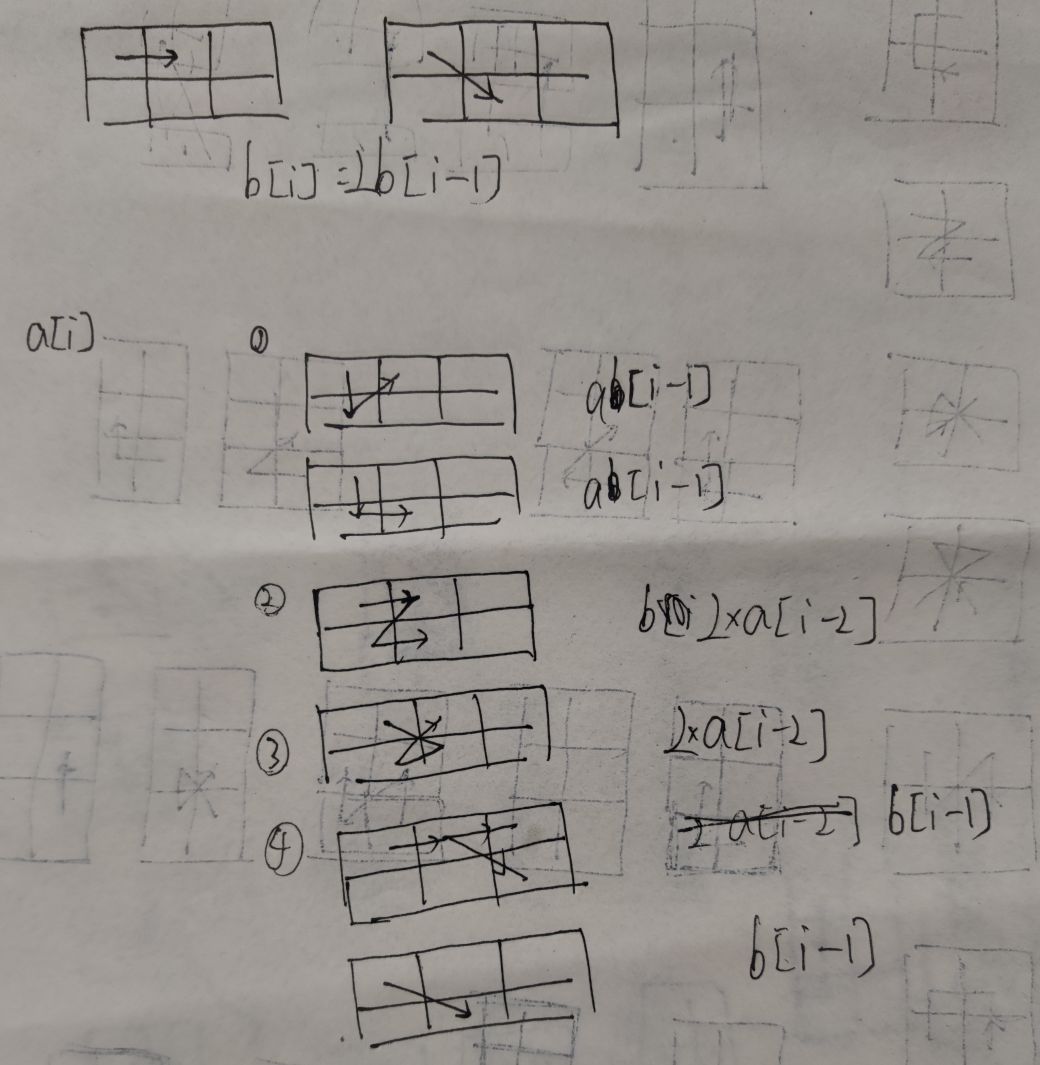
由此得到

b[i]=b[n-1]

a[i]=a[i-1]+a[i-1]+2*a[i-2]+2*a[i-2]+b[i-1]+b[i-1]

讨论完边界情况后我们需要讨论从中间出发的情况：

当n=5时，我选择从第二列第一行出发：

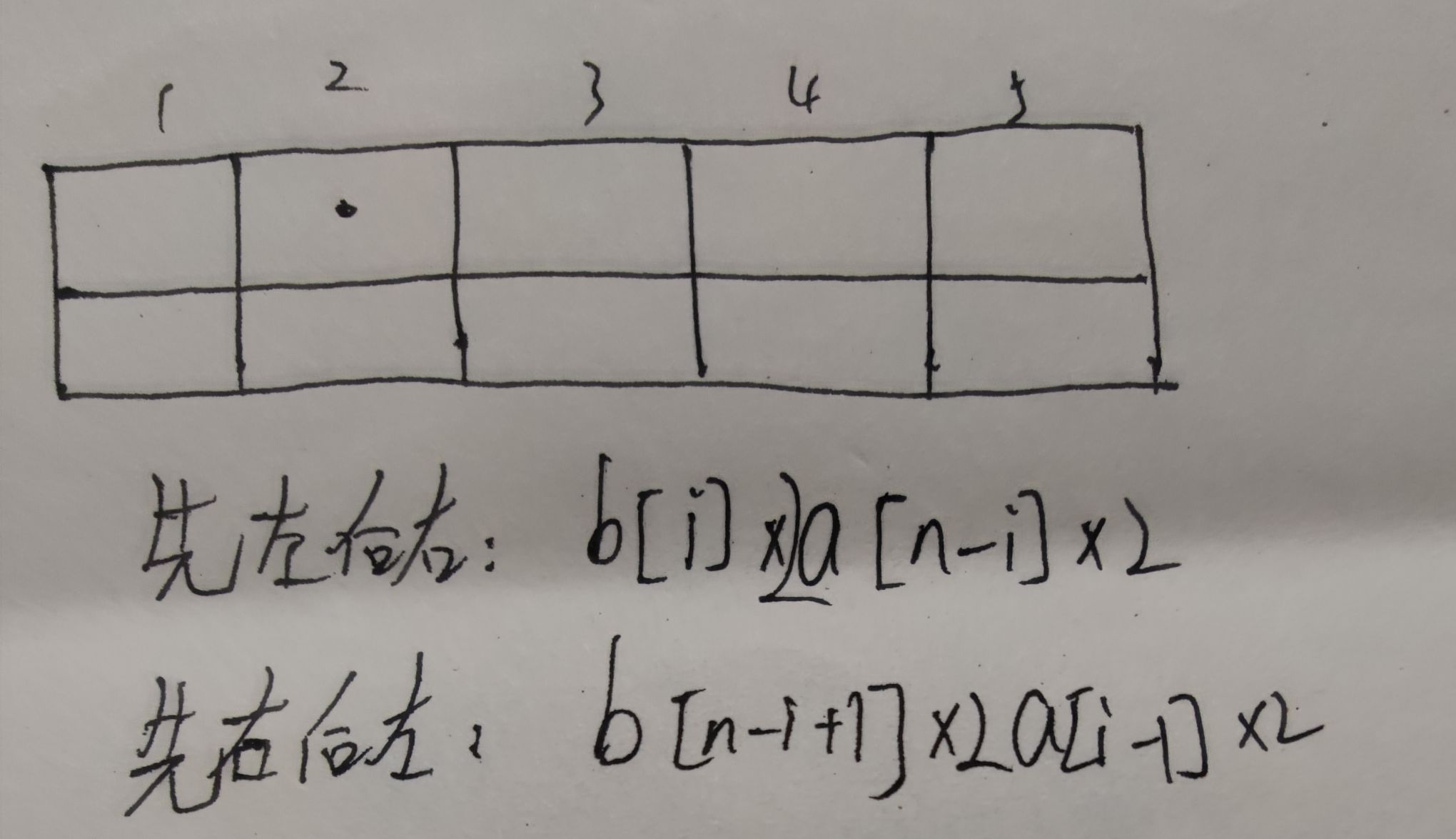
上图中两式第一个二是因为从第二列第一行回到第二列第二行时，又从第二列第二行出发到右或左侧分别有斜方向和横方向两种情况

第二个二是因为可以分别把第二列第二行或者第二列第一行作为起点

由此可以贴上代码：

#includeusing namespace std;
#define mod 1000000007
int n;
long long int  a[1000];//表示从起点出发遍历全部格子的方案数
long long int b[1000];//表示从起点出发遍历全部格子且终点与起点同列
long long int sum;
int main()
{
	cin >> n;
	a[1] = 1;
	b[1] = 1;
	a[2] = 6;
	b[2] = 2;
	for (int i = 3; i <= n; i++)
	{
		b[i] = 2 * b[i - 1] % mod;
		a[i] = ((2 * b[i - 1]) % mod + (4 * a[i - 2]) % mod + (2 * a[i - 1]) % mod) % mod;
	}
	for (int i = 2; i < n; i++)
	{
		sum += ((4 * b[n - i + 1] % mod * a[i - 1] % mod) % mod + (4 * b[i] % mod * a[n - i] % mod) % mod) % mod;
	}
	sum = (sum + ((a[n] * 4) % mod)) % mod;
	cout << sum;
	return 0;
}