1433 危险系数 较为省空间的解题方法

解题思路:根据题意，如果某一点为”关键点“，那么所有路径中都会出现它。所以可以设置一个time数组表示某一点被访问的次数，如果正好等于路径数，那么它就是”关键点“。寻找路径可以使用DFS。

我们可以用链式向前星存储图，以达到省空间的目的，同时也能在一定程度上节省时间。

有关链式向前星的讲解，请点击这里。

注意事项:

我当时犯了2个错误：

1.dfs函数一开始就无条件tme[cur]++；实际上cur能不能到目的地还不一定呢；

2.把cnt+=dfs(to,e)弄成if(dfs(to,e))    cnt++;个人认为，这样做其实是在求某点邻接边中能到达目标节点的总数。比如下面的图，大家可以模拟一下（那堆带箭头的是递归过程）

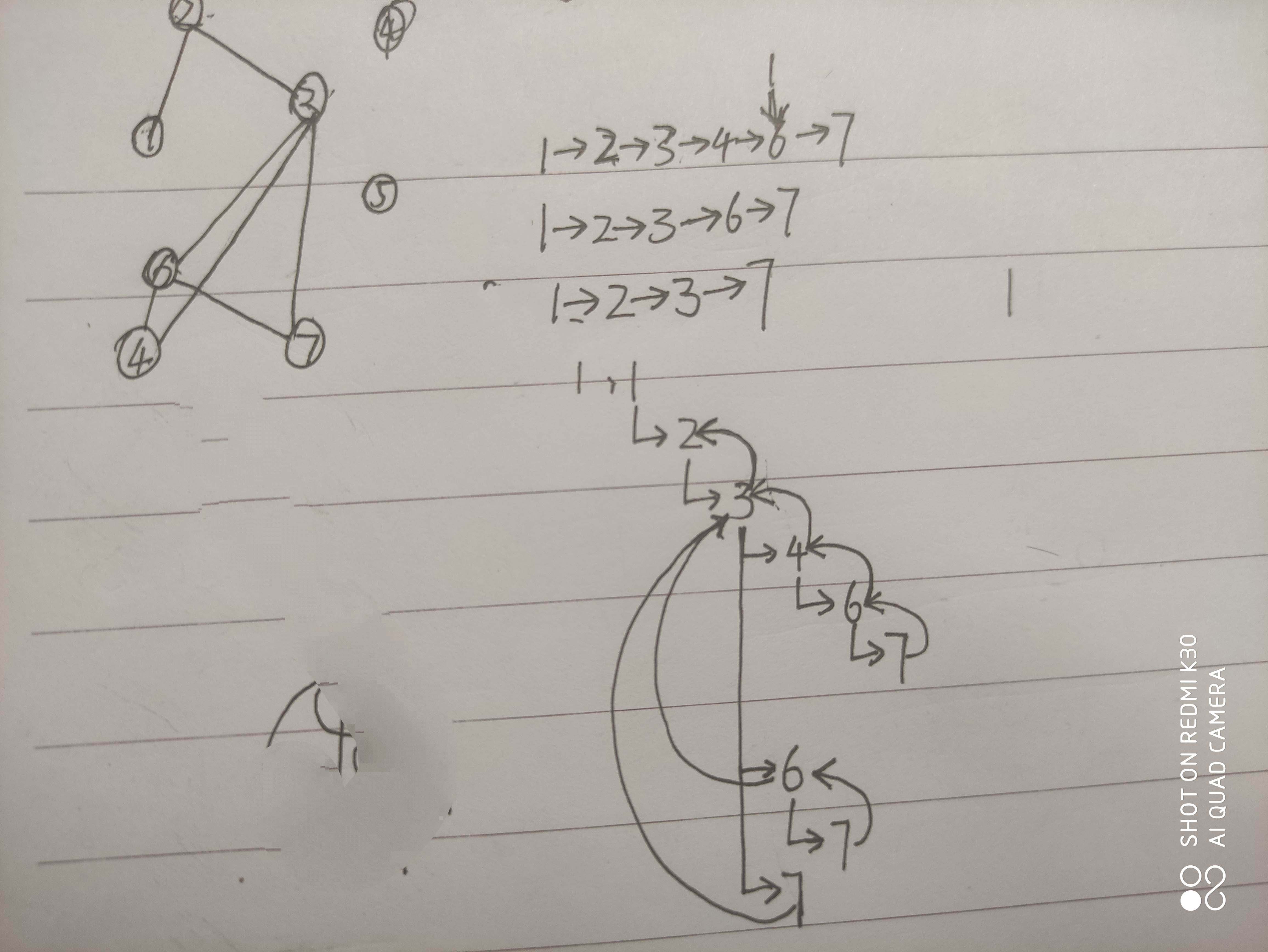
还有注意起点和终点不要算进去。

参考代码:

#include<cstdio>
#include<algorithm>
#include<vector>
const int M=1002,M_EDGE=2001;
using namespace std;
struct graph {
    int next,to;
    graph():next(-1),to(-1) {}
    graph(int n,int t):next(n),to(t) {}
};
vector<graph> G;
int n,fir[M],tme[M],cnt=0;
bool vis[M];
//构建边
void add(int u,int v,int &m) {
    G[m]=graph(fir[u],v);
    fir[u]=m++;
}

int dfs(int cur,int e) {
    if(cur==e) {
        cnt++;
        return 1;
    }
    //cnt:经过当前节点的路径数
    int cnt=0;
    for(int i=fir[cur]; i!=-1; i=G[i].next) {
        int to=G[i].to;
        if(!vis[to]) {
            vis[to]=1;
            cnt+=dfs(to,e);
            vis[to]=0;
        }
    }
    tme[cur]+=cnt;
    return cnt;
}

int main() {
    int m,t=0,res=0;
    scanf("%d%d",&n,&m);
    fill(fir+1,fir+n+1,-1);
    //以下为初始化
    G.resize(min(m*(m-1),M_EDGE));
    for(int i=0; i<m; i++) {
        int u,v;
        scanf("%d%d",&u,&v);
        add(u,v,t);
        add(v,u,t);
    }
    int s,e;
    scanf("%d%d",&s,&e);
    vis[s]=1;
    dfs(s,e);
    if(cnt==0)
        printf("-1");
    else  {
        for(int i=1; i<=n; i++) {
            if(tme[i]==cnt&&i!=s&&i!=e) {
                //printf("%d ",i);
                res++;
            }
        }
    }
    printf("%d",res);
    return 0;
}