1471: 蓝桥杯基础练习VIP-矩形面积交(C++代码)

解题思路:

1、先判断两个矩形是否有重合部分

2、利用排序计算重合部分面积（中间两坐标差值之积）

1、如何判断

假设 a1 为矩形A的左下端点，a2 为A的右上端点

同样的，假设 b1, b2分别为矩形B的左下和右上端点

那么A与B有重合部分的充要条件是，任一矩形的左下端点均在令一矩形的右上端点的左下方

即，a1在b2的左下方，且b1在a2的左下方

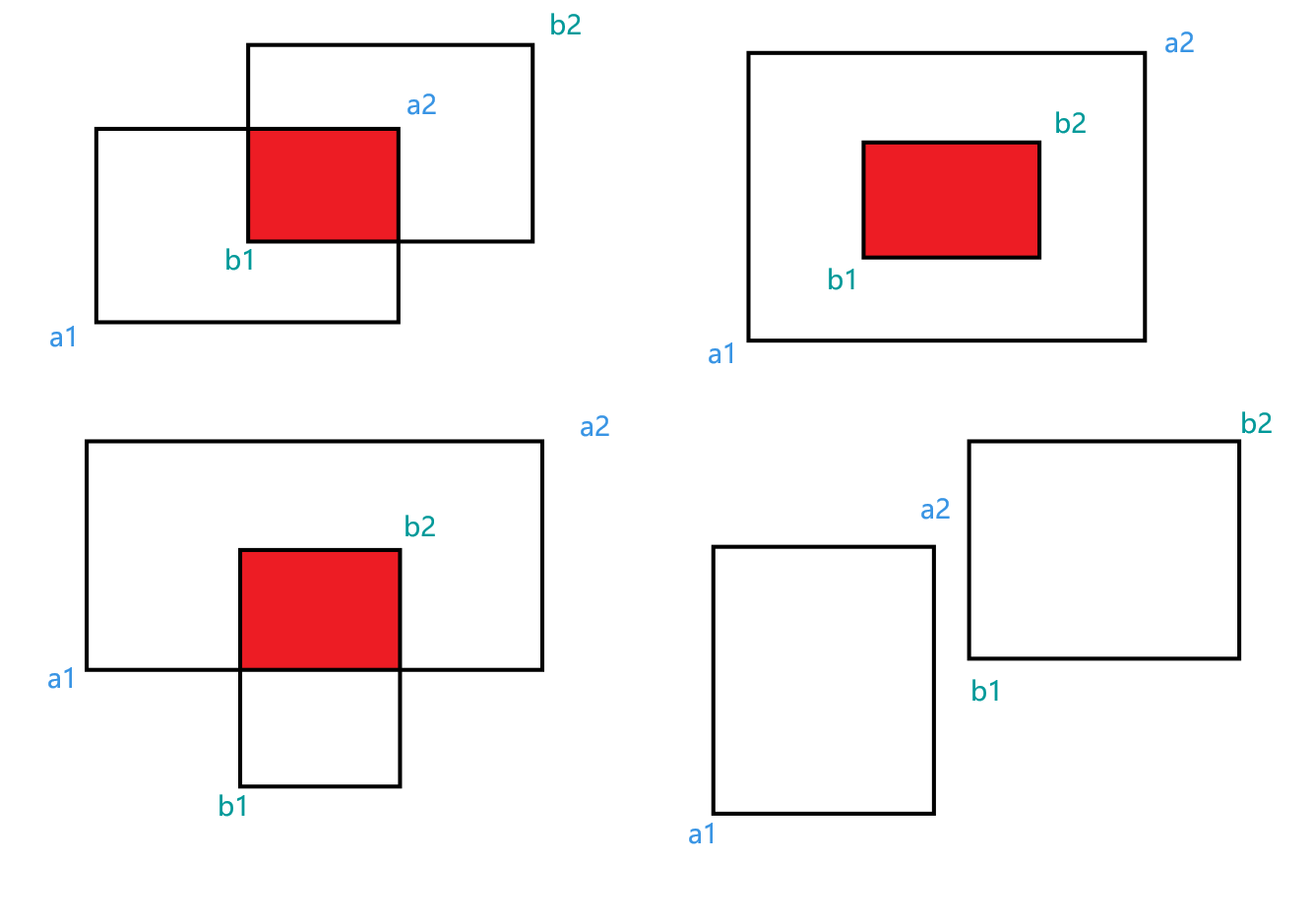
矩形的左下端点坐标是输入的两横纵坐标中较小值的组合，相对的，右上端点是较大值的组合

一个点的横纵坐标均比另一个的坐标小，则前者在后者的左下方

2、如何计算重合部分面积

将输入四个横坐标与纵坐标排序，位于中间的两组坐标表示的即为重合部分的矩阵

排序后的中间两坐标差值之积即为所求面积

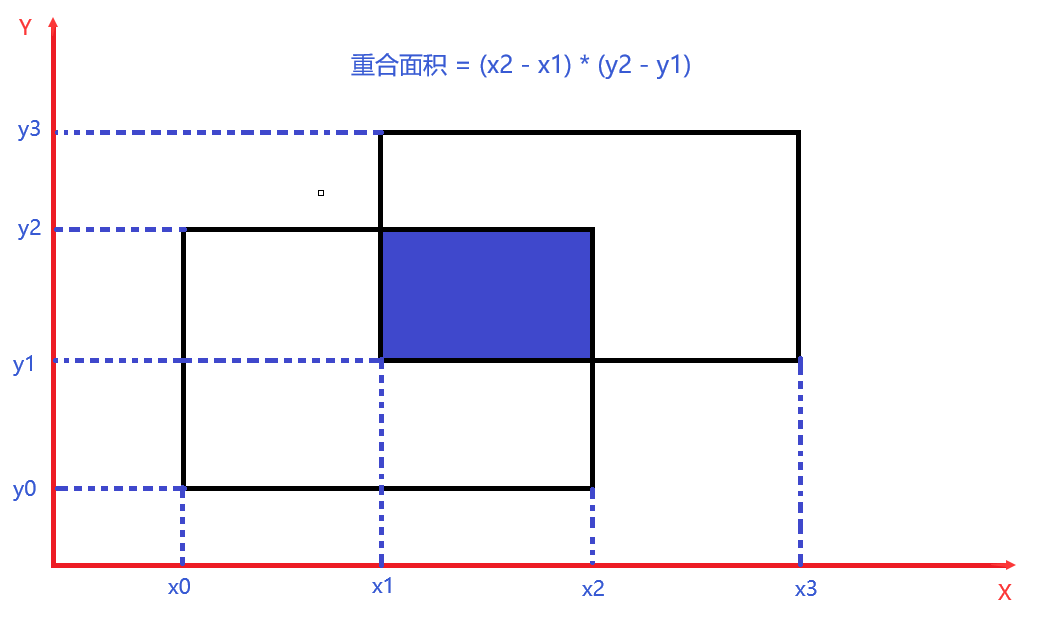
参考代码:

#include <bits/stdc++.h>
 
using namespace std;
 
class point         //定义"点"类，可用大小为2的数组代替
{
public:
    double x;
    double y;
};
 
bool mycheck(point a, point b)              //函数：判断点a是否在点b左下方
{
    return (a.x < b.x && a.y < b.y);
}
 
int main()
{
    double x[4];                //记录输入的横坐标
    double y[4];                //记录输入的纵坐标
 
    point a1, a2, b1, b2;       //定义矩阵A与B的左下和右上端点，1为左下，2为右上
 
    for (int i = 0; i < 4; i++)     //循环输入
    {
        cin >> x[i] >> y[i];
    }
    //寻找两矩阵的左下右上端点
    a1.x = fmin(x[0], x[1]), a1.y = fmin(y[0], y[1]);
    a2.x = fmax(x[0], x[1]), a2.y = fmax(y[0], y[1]);
 
    b1.x = fmin(x[2], x[3]), b1.y = fmin(y[2], y[3]);
    b2.x = fmax(x[2], x[3]), b2.y = fmax(y[2], y[3]);
 
    double ans = 0;             //定义答案
    if (mycheck(b1, a2) && mycheck(a1, b2))     //判断是否重合
    {
        sort(x, x + 4);                         //横坐标排序
        sort(y, y + 4);                         //纵坐标排序
        ans = (x[2] - x[1]) * (y[2] - y[1]);    //计算答案
    }
    printf("%.2f\n", ans);                      //输出
    return 0;
}