蓝桥杯2013年第四届真题-格子刷油漆-题解（Python代码）动态规划

解题思路:

DFS会超时

分两类来看，我们设a[i],b[i]两个数组，这里划分的依据是终点的类型不同，大家往下看就明白了

a数组表示长度为i的格子（也就是2*i的格子图）从某一点出发，终点任意（这里注意下，是终点任意，所以a数组对b数组有个包含关系）的方案数目

b数组表示长度为i的格子，从某一点出发，最终回到同一列的方案数

以上把数组含义介绍好了
·····

我们还需要注意一点，因为起始点是任意的，我们也需要分开来看

1、当出发点是四个顶点之一（2*i的矩形当然只有四个顶点了）

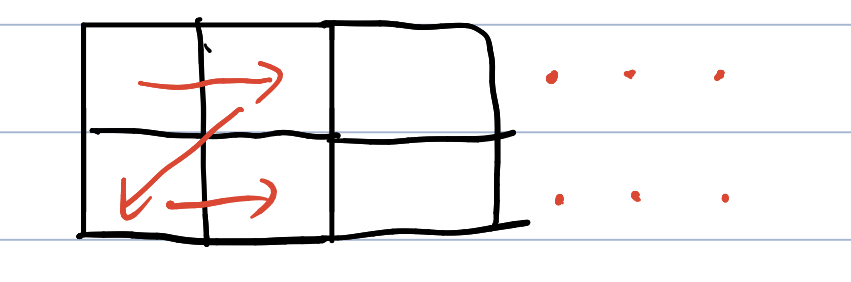
来看一下长度为2的时候的例子：

b[i]=b[i-1]*2

假如我们从左上角的顶点出发，我可以直接往右走，也有往右下走，（不可以往下走，我们在讨论最终回到同一列的情况），那其实就是在计算b[i-1]了吧。为什么要乘2呢，因为我们还可以从左下角出发。

a[i]=a[i-1]*2+b[i]+2*2*a[i-2]

我们分开来看，a这个数组其实分为两部分，第一部分是终点不会和起始点同一列，另一部分就是b[i]了，所以这个➕b[i]很直观，关键是a[i-1]*2+2*2*a[i-2]怎么来的。

先看下a[i-1]*2,这个和b[i]的推导几乎一致，我们想不回到同一列，假设我们还是从左上角出发，那可以先往下走，把这一列占满，那现在就剩i-1列了，这又回到了计算a[i-1]，乘2怎么来的呢，一样是因为我们还可以从左下角出发。

再来看a[i-2]*4。前面说我想不回到同一列，直接往下走。我也可以先到第二列的任意一个格子，再回到第一列，然后再回到第二列，这样的话前两列满了，我们就计算a[i-2]就可以了，4是因为有四种方案把前两列占满。

2、当出发点在中间的时候

这种情况只需要理解一句话，假设我在第i列

那我需要计数从出发点向左或者向右并且回到出发点同一列，再往反方向做终点任意的运动的方案数即可，代码很清楚，我分开来写了。

注意事项:没什么太需要注意的，能理清楚关系怎么推来的就可以了，a[1]与b[1]并不是2，这个得自己理解下。

我有写的不清楚的地方还请大家指正

参考代码:

n=int(input())
mod=1000000007
a=[0 for i in range(n+1)]
b=[0 for i in range (n+1)]
a[1]=1
a[2]=6
b[1]=1
b[2]=2
for i in range(3,n+1):
    b[i]=b[i-1]*2
    a[i]=a[i-1]*2+b[i]+4*a[i-2]
ans=a[n]*4%mod
for i in range(2,n):
    ans=(ans+b[i]*a[n-i]*4)%mod
    ans=(ans+b[n-i+1]*a[i-1]*4)%mod
print(ans%mod)