经典递归题:汉诺塔(Hanoi)不同角度深入探究(C/C++/Java版)

经典原型:

        汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

抽象数学问题:

        从左到右有A、B、C三根柱子，其中A柱子上面有从小叠到大的n个圆盘，现要求将A柱子上的圆盘移到C柱子上去，期间只有一个原则：一次只能移到一个盘子且大盘子不能在小盘子上面，求移动的步骤和移动的次数.

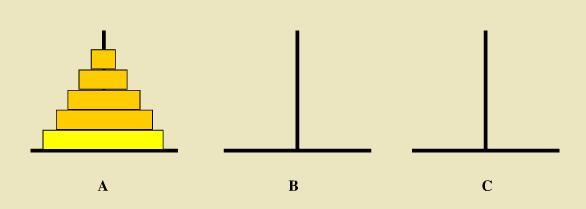
基础思路:

    利用B、C两根柱子的来实现交换原则:一次只能移到一个盘子且大盘子不能在小盘子上面;

其次就是先放哪根柱子，后放哪根柱子的问题，递归设计过程：

 1.通过给定盘子的数目n，先递归到最底层数n=1的那一层实质上就是我们界定此时只对一个盘子向B/C移动，n为奇数，打印A->C，n为偶数，打印A->B;

 2.n=1的底层打印结束后，回到上一层，因为我们每一层递归的时候a,b,c的位置都是按规则排列的，所以回到这一层直接打印A->B/C(也就是放到另一个空柱子上);

 3.最底2层是实现结束后，到达B/C柱子上都有一个盘子，只不过一个大一个小，因此我们在回到上一层的时候就只需要移动B盘C盘，A盘不动，打印B(C)->C(B);

 4.根据以上三条规则的界定，就可以实现整个递归过程的调用和打印，“先深入，后浅出”的模式，以此类推的实现整个过程；   

C语言最简洁的方法来实现最基础的汉诺塔问题(示例代码):

#include void hanoi(int m,char a,char b,char c){
   if(m == 1)
       printf("%c->%c\n",a,c);
   else
   {
       hanoi(m - 1, a, c, b);
       printf("%c->%c\n",a,c);
       hanoi(m - 1, b, a, c);
   }
}
int main(){
   int x;
   scanf("%d",&x);
   hanoi(x,'A','B','C');
   return 0;
}

运行截图:

探究递归过程的规律:

     （1）n == 1         

       　　　　　　第1次  1号盘  A---->C       sum = 1 次

       (2)  n == 2

       　　　　　　第1次  1号盘  A---->B

      　　　　　　 第2次  2号盘  A---->C

       　　　　　　第3次  1号盘  B---->C        sum = 3 次

　　（3）n == 3

　　　　　　　　第1次  1号盘  A---->C

　　　　　　　　第2次  2号盘  A---->B

　　　　　　　　第3次  1号盘  C---->B

　　　　　　　　第4次  3号盘  A---->C

　　　　　　　　第5次  1号盘  B---->A

　　　　　　　　第6次  2号盘  B---->C

　　　　　　　　第7次  1号盘  A---->C        sum = 7 次

不难发现规律：

                            1个圆盘的次数 2的1次方减1

                            2个圆盘的次数 2的2次方减1

                            3个圆盘的次数 2的3次方减1

                             ......

                             n个圆盘的次数 2的n次方减1

 故：移动次数为：2^n - 1

改进程序：添加计数功能，来精准出每一次移动的部数。

改进后C语言代码:

#include int sum = 0;//用一个全局变量计数
void hanoi(int m,char a,char b,char c){
   if(m==1)
   {
   	sum++; 
       	printf("第%d次移动：%c->%c\n",sum,a,c); 	
   }
   else
   {
      	hanoi(m - 1, a, c, b);
   	sum++; 
       	printf("第%d次移动：%c->%c\n",sum,a,c); 
       	hanoi(m - 1, b, a, c);
   }
}
int main(){
   int x; 
   scanf("%d",&x);
   hanoi(x,'A','B','C');
   return 0;
}

运行截图:

例如：我们可以准确看出在n=9的执行条件下，第60次移动就是C->B：

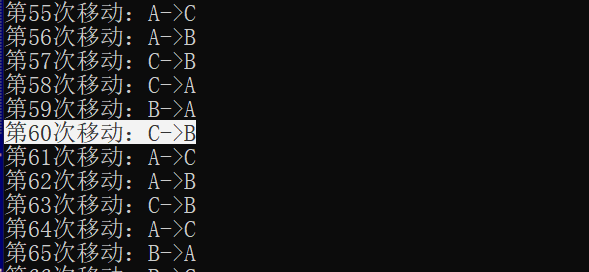
最后用java来总结一遍：

import java.util.Scanner;

public class Hanoi {
	public static int sum = 0;//静态变量
	public static void main(String[] args)
	{
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		sc.close();
		hanoi(n,'A','B','C');
	}
	public static void hanoi(int n,char a,char b,char c)
	{
		if(n == 1)
		{
			sum++;
			System.out.println("第"+sum+"次移动："+a+"->"+c);
		}
		else
		{
			hanoi(n-1,a,c,b);
			sum++;
			System.out.println("第"+sum+"次移动："+a+"->"+c);
			hanoi(n-1,b,a,c);
		}
	}
}

汉诺塔问题解法很多，欢迎大家留言自己的思路或者更好的代码实现！！