蓝桥杯2013年第四届真题-大臣的旅费-题解图的遍历-（Java代码）

以下部分图片与文字来自《啊哈算法》-----

深搜与广搜是针对图的遍历而言的。

使用深度优先搜索来遍历图的具体过程是：首先从一个未经过的起点作为顶点，沿着当前顶点去尝试访问其他未走过的顶点；当没有未访问过的顶点时，则回到上一个顶点，继续试探访问别的顶点，直到所有的顶点都访问过。

要遍历图的首要任务是存储图 ，最常用的方法是用一个二维数组arr来存储，如下：

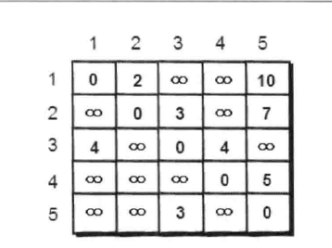
图中数据与本题无关。

arr[i][j]==0表示i到j没有路线，否则为i到j的距离。

图可以分为两种：有向图、无向图

有向图只能从i到j，不能从j到i。

无向图是互通的。

以上是对于图的遍历的一个简陋的说明，接下来是关于本题的思路。

思路分析：

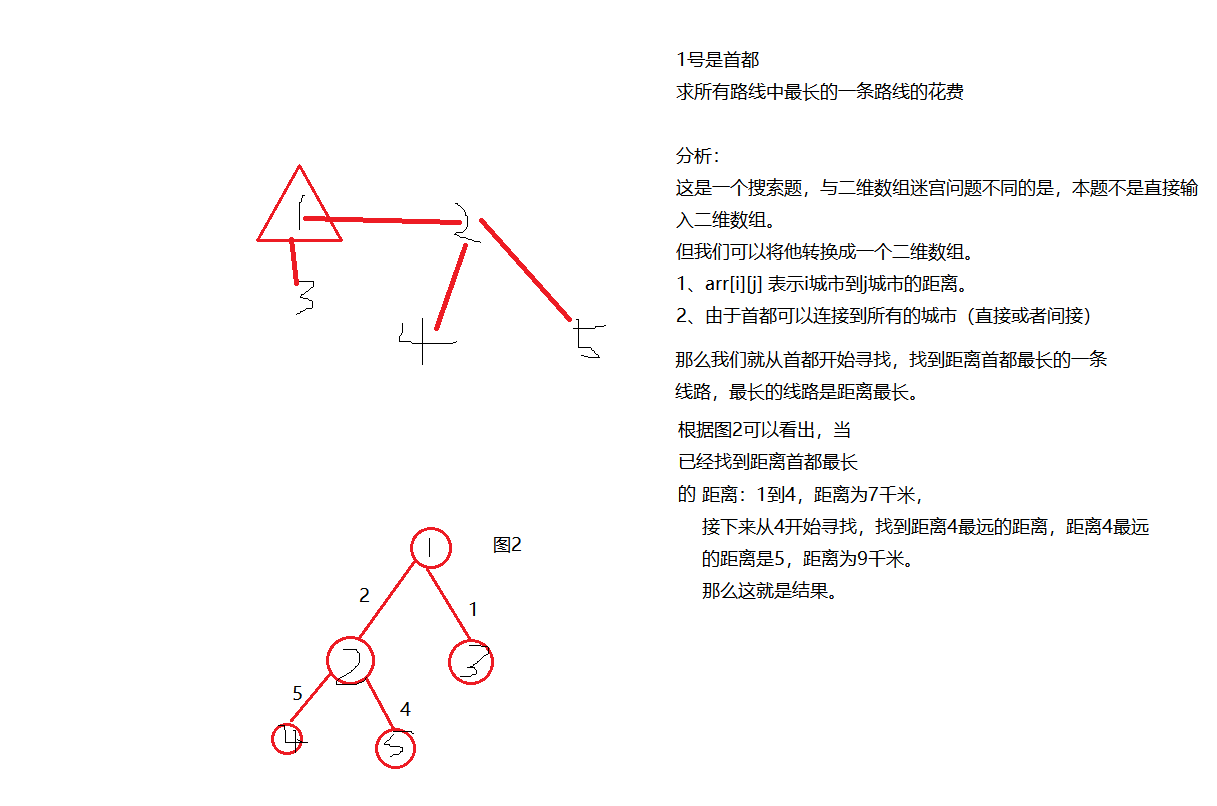
需要注意的地方：

1、题目说是连接各个城市，所以在用二维数组存储图时，不仅有arr[pi][qi]=di;还有arr[qi][pi]=di;

2、使用flag[]标记走过的路线时，因为是有向图，所以flag[pi] 和flag[qi] 都要标记。因为用二维数组flag[][]会内存超限，所以改用一维数组，这题应该有更好的解法，使用dfs已经在内存超限的边缘了。。。

3、在第一次搜索后，需要maxKil=0。

参考代码

import java.util.Scanner;

public class Main {

	/**
	 * @param args
	 */
	public static int maxKil=0,mZ=0;//最大的距离,第一次dfs得到最大距离对应的城市号
	public static int arr[][];//存储输入数据，即城市之间的距离
	public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		int n=sc.nextInt();
		arr=new int[n][n];
		int flag[]=new int[n];//标记是否走过，使用一维数组
		for (int i = 0; i <n-1; i++) {//给arr存储数据
			int pi=sc.nextInt()-1;
			int qi=sc.nextInt()-1;
			int di=sc.nextInt();
			arr[pi][qi]=di;
			arr[qi][pi]=di;
		}
		//第一次dfs,目的是找到距离起点最远的那个点，并赋值给mZ
		dfs(0, 0,flag);
		//System.out.println("mZ:"+mZ);
		
		flag[0]=0;//第二次dfs，取消第一次的起点标记
		maxKil=0;
		dfs(mZ, 0, flag);
		System.out.println(getCost(maxKil));
}
	//搜索
	public static void dfs(int detp,int maxK,int flag[]) {
		for (int i = 0; i < arr.length; i++) {
			if (detp==arr.length) {
				return ;
			}
			if (maxK>maxKil) {//可能会出现未全部遍历完 得到的maxK>maxKil的情况
				maxKil=maxK;
				mZ=detp;
			}
			if (arr[detp][i]!=0 && flag[i]==0) {//有路线，且没走过
				flag[detp]=1;
				flag[i]=1;
				dfs(i,arr[detp][i]+maxK,flag);
				flag[detp]=0;
				flag[i]=0;
			}
		}
		return ;
	}
	
	//根据千米获得需要的费用
	public static int getCost(int k) {
		int sum=0;
		for (int i = 1; i <=k; i++) {
			sum+=(i+10);
		}
		return sum;
	}
	
}