蓝桥杯2013年第四届真题-大臣的旅费-题解（C++代码）

解题思路:

1. 1.构建图

2. 2.dijkstra 从任意一个点出发，找到距离这个点最远的点，再从这个点出发，找到一条最长的路

3. 3.根据路的长度求出旅费

为什么要找到某个点的最远点? 而不是从任意的边缘的某个点为起点直接寻找最长路？

如图：

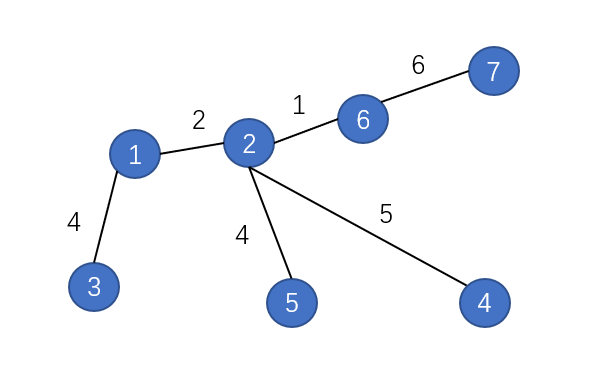
假如随便找一个边缘的点为起点，如4号点，那么它得到的最长路是：4-2-6-7， 总长度为5 + 1 + 6 = 12；

而实际上，整个图中最长的路应该是：7-6-2-1-3，总长度为6 + 1 + 2 + 4 = 13;

所以不能在图边缘任意取一个点作为起点出发。

注意事项:

参考代码:

#include#include#include#include#include#includeusing namespace std;
#define ll long long int
const int INF = 0x3f3f3f3f;
const int MAXN = 1e6 + 9;
int n;
struct Edge
{
    int to, nxt;
    ll w;
}edge[MAXN];
int head[MAXN], t = 0;
void init()
{
    memset(head, -1, sizeof(head));
    t = 0;
}
void addEdge(int u, int v, ll w)
{
    edge[t].to = v;
    edge[t].w = w;
    edge[t].nxt = head[u];
    head[u] = t++;
}
ll dis[MAXN];
int vis[MAXN];
int dijkstra(int x)
{
    memset(dis, 0, sizeof(dis)); dis[x] = 0;
    memset(vis, 0, sizeof(vis)); vis[x] = 1;

    int distan = 0;
    int point = x;
    queue q;
    q.push(x);
    while(!q.empty())
    {
        int u = q.front(); q.pop();
        if(dis[u] > distan) // 记录最远点
        {
            distan = dis[u];
            point = u;
        }

        for(int i = head[u]; i != -1; i = edge[i].nxt)
        {
            int to = edge[i].to;
            ll w = edge[i].w;

            if(!vis[to] && dis[to] < dis[u] + w)
            {
                dis[to] = dis[u] + w;
                vis[to] = 1;
                q.push(to);
            }
        }
    }
    return point;
}
int main()
{
    cin >> n;
    int u, v; ll w;
    init();
    for(int i = 1; i < n; i++)
    {
        cin >> u >> v >> w;
        addEdge(u, v, w);
        addEdge(v, u, w);
    }

    int st = dijkstra(1);  // 从任意一个点出发（这里从1出发），找到离这个点最远的点st
    dijkstra(st);  // 从st出发，能求出图中最长的一条路

    int distan = 0;
    for(int i = 1; i  dis[i] ? distan : dis[i];
    }


    ll ans = 0;
    if(distan % 2 == 0)
    {
        ans = distan / 2;
        ans = ans * (distan + 1);
        ans = ans + distan * 10;
    }
    else
    {
        ans = (distan + 1) / 2;
        ans = ans * distan;
        ans = ans + distan * 10;
    }
    cout << ans << endl;
    return 0;
}