关于圆的面积 （C语言代码）

解题思路:

    两圆相交分如下集中情况：相离、相切、相交、包含。

    设两圆圆心分别是O₁和O₂，半径分别是r1和r2，设d为两圆心距离。又因为两圆有大有小。

    相离相切的面积为零

d=sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));	
if(d>=r1+r2) //相离或外切
    return 0;

包含的面积就是小圆的面积了

if(r1>=d+r2) //内切或内含
    return PI*r2*r2;
if(r2>=d+r1)  //内切或内含
    return PI*r1*r1;

接下来看看相交的情况。

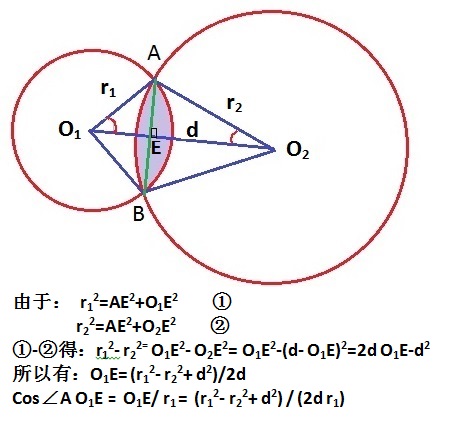
    相交面积可以这样算：S=扇形O₁AB - △O₁AB + 扇形O₂AB - △O₂AB，

    这两个三角形组成了一个四边形，可以用两倍的△O₁AO₂求得，

    所以答案就是两个扇形-两倍的△O₁AO₂。

    要求出扇形的面积，要知道扇形的圆心角。

    小圆包含的扇形的圆心角为2*ang1           //ang1表示∠AO₁O₂=∠AO₁E
    ang1=acos((r1^2-r2^2+d^2)/(2*r1*d))    //ang1表示∠AO₁O₂ ，求法如上图下方公式所示。 
    ang2=acos((r2^2-r1^2+d^2)/(2*r2*d))    //ang2表示∠AO₂O₁

    扇形O₁AB面积=pi*r1*r1*2*∠AO₁O₂ / (2*pi)=ang1*r1*r1  
    同理： 
    扇形O₂AB面积=ang2*r2*r2 

    两倍的△O₁AO₂=2*r1*d*sin(∠AO₁O₂)/2=r1*d*sin(ang1) 

    则S=ang1*r1*r1+ang2*r2*r2-r1*d*sin(ang1)

ang1=acos((r1*r1-r2*r2+d*d)/(2*r1*d));  //第一个圆心角的一半 
ang2=acos((r2*r2-r1*r1+d*d)/(2*r2*d));  //第二个圆心角的一半
return ang1*r1*r1+ang2*r2*r2-r1*d*sin(ang1); //两个扇形面积之和-两倍的△O1AO2

参考代码:

#include <stdio.h>
#include <math.h>
#define PI acos(-1.0)
double Area(double x1,double y1,double x2,double y2,double r1,double r2)
{
	double d;
	double ang1,ang2;
	d=sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));	
	if(d>=r1+r2) //相离或外切
		return 0;
	if(r1>=d+r2) //内切或内含
		return PI*r2*r2;
	if(r2>=d+r1)  //内切或内含
		return PI*r1*r1;	
	//两个圆相交情况 
	ang1=acos((r1*r1-r2*r2+d*d)/(2*r1*d));  //第一个圆心角的一半 
	ang2=acos((r2*r2-r1*r1+d*d)/(2*r2*d));  //第二个圆心角的一半
	return ang1*r1*r1+ang2*r2*r2-r1*d*sin(ang1); //两个扇形面积之和-两倍的△O1AO2	
}
int main()
{
	double x1,y1,x2,y2,r1,r2;	
	double area;
	int n;
	scanf("%d",&n);
	while(n--)
	{
		scanf("%lf%lf%lf%lf%lf%lf",&x1,&y1,&x2,&y2,&r1,&r2);
		area=Area(x1,y1,x2,y2,r1,r2);	
		printf("%.3f\n",area);
	}	
	return 0;
}