完美解决质因子(素数+因数)（C语言代码）

测试环境:

Windows 10 China Huawei Source Insight 4.0 

Linux Debain Ubuntu/Kali g++

程序代码:

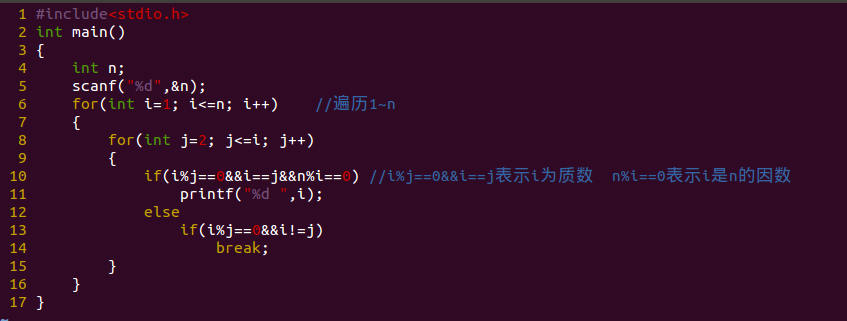
多组测试:

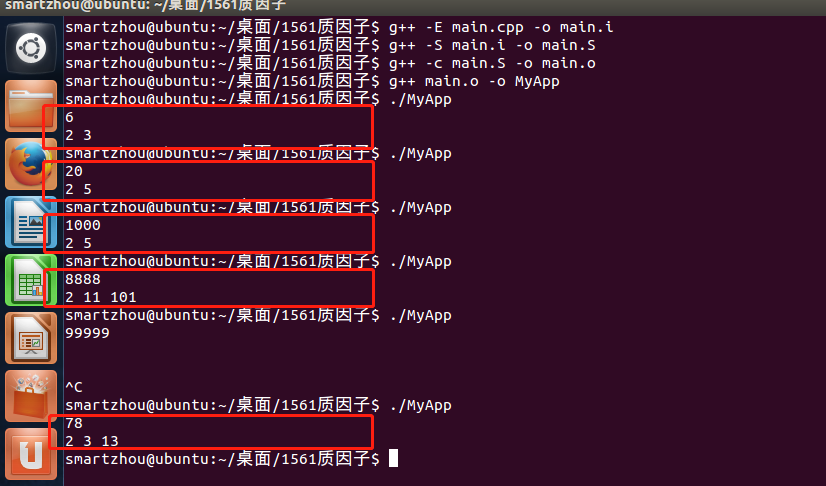
解题思路:

质因数即质数+因数。质数又叫素数。

判断因数很简单，如果i 是n的因数，则n%i==0.

所以重点就是判断素数!

推荐以下经典素数好文:

素数经典解法

素数巧解

假如i是素数,则i不能整除2~i之间的所有数,定义一个变量j,取 2~i之间所有值。如果中间的数都不能除尽，

那么一起循环到最后一次j变成i时,i%j==i%i==0 这个时候i==j ,i就一定是素数。如果在j=0~i的循环中途

就出现i%j==0,说明i一定不是素数.

代码分析:

第一次循环:

for(int i=1; i<=n; i++) 为遍历1~n之间所有的数

第二次循环:

 for(int j=2; j<=i; j++) 

j取2~i之间，如果一个数i 对于2~i之间所有的数都不能整除，则i是素数。

即如果i % j！=0则i是素数。

我采用的方法是穷举反证:

如果i%j!=0素数，那么当循环结束的时候i==j，i%j==i%i==0。则i是素数 

再判断 n%i ==0 知i又是因子

如果i%j==0 &&i !=j 说明在循环的过程中，出现了整除情况，说明i不是素数，跳出即可。
注意事项:

参考代码:

#include <stdio.h>
int main() 
{
	int n; 
	scanf("%d",&n);
	for(int i=1; i<=n; i++)  //遍历1~n 
	{
		for(int j=2; j<=i; j++)
		{
			if(i%j==0&&i==j&&n%i==0)
			{
				printf("%d ",i);
			}
			else if(i%j==0&&i!=j)
			{
				break;
			} 				
		}	
	} 
}