母牛的故事 （C++代码）

解题思路:

        将此题中按照 第6年 画出树状图: （数字为奶牛的年龄）

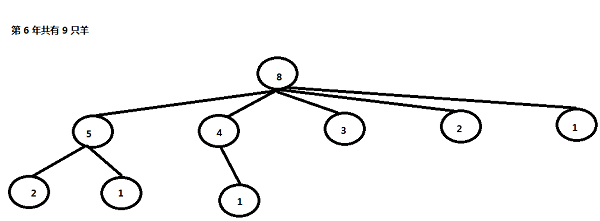
        由此可见: 只要求得第一个奶牛的子孙数量 + 自身 就是 第六年的答案:

        第一个奶牛的子孙的数量 = 孩子的数量 + 能生产的孩子的子孙数量。

        依此类推 此题适合使用递归方式来解题:

    递归公式 :
        我们设T(age) 为 求 年龄为 age 的奶牛的子孙的数量，则
        T(age) = 0  , 当age < 4 时, 代表不能生产
        = age - 3 , 当 4=<age <7 的时候, 因为他们的只有孩子
        = T(4) +.........+T(age-3) + age-3 , 当 7=<age有孙子  
          由递归公式可得: 第六年的奶牛的数量为 T(6+2) + 1 个

        优化:

                递归当中存在很多的重复的计算, 比如计算 第 6 年 和 第 7 年的时候, 都会重复的计算 T(5),T(4) ,                     而伴随这n的增大, 重复的计算的次数就越多, 因此设置一个缓存, 表示计算过指定的年龄的奶                            牛的数量, 直接从缓存当中取出, 不用在去递归了。

注意事项:

                这种树状结构能画出的图, 有时候使用递归方式能写出简洁的代码, 若小规模问题是大规模问题的                    一 个子集, 明显可以设置一个缓存去优化递归的深度。

参考代码:

#include <iostream>
using namespace std;

int ageMap[58];  //定义一个缓存用于存储已经计算过的值了
long long func(int);

int main()
{
	int n;
	while(cin >> n && n)
	{
		long long sum = func(n+2);
		cout << (sum + 1) << endl;
	}
	return 0;
}


/* age 的值 为 n+2 , 代表第一只奶牛的年龄 */
long long func(int age) 
{
	
	if(ageMap[age])				   // 已经计算过了, 从缓存当中取得
		return ageMap[age];

	long long sum = age -3;        // 当前奶牛的孩子的数量;
	for(int i = 4; i<=age-3; ++i)  // 遍历能生产的孩子, 获取其孩子的子孙数量
		 if(!ageMap[i])
		 	sum  += func(i);     
		 else
		 	sum  += ageMap[i];     // 从缓存当中读取值 

	ageMap[age] = sum;			   // 记录缓存
	return sum;
}