聊聊差分数组

聊聊差分数组

       有这么一类题型，给你一个数组，再给定你一个区间，这个区间的数统一增加一个值，再给定你一个区间，求这个区间中所有数的和。

       什么？听不明白？

       好的我说详细一点，你需要输入一个n，然后输入n个元素，接着你需要输入一个区间和一个值，分别为L,R,W，L为左边界，R为右便捷，W为值，接着数组元素属于这个区间的值统一增加W，接着再输入一个区间L,R，求L到R中所有元素的和。

        那我们废话不多说，直接上代码

       代码1：

#include<iostream>
using namespace std;
int main(){
	int a[10000],n;
	int l,r,w;
	long long sum=0;
	cin>>n;
	for(int i=0;i<n;i++){
		cin>>a[i];
	}
	cin>>l>>r>>w;
	for(int i=l-1;i<r;i++){
		a[i]+=w;
	}
	cin>>l>>r;
	for(int i=l-1;i<r;i++){
		sum+=a[i];
	}
	cout<<sum;
	return 0; 
}

       验证一下结果，正确！

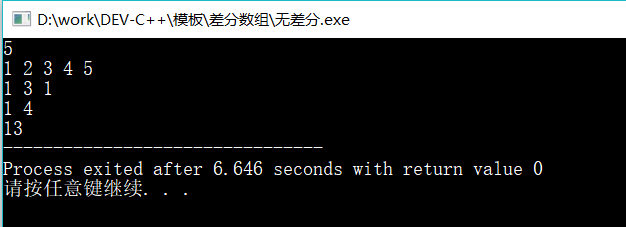
        很简单是不是，那好，我修改一下要求，在我们输入L,R,W三个值的时候，我要求多组输入，同时输出区间L,R的和的时候，我要求多组输出，怎么样？

       你想想也是很简单的嘛，加一个t，输入t，再弄一个while（t--），完美控制到了多组的输入，然兴冲冲的提交了代码。

       结果：

       其实，这里有一个问题，当我们在输入多组L,R,W的时候，我们是需要利用for循环来实现的，当我们多组输入的时候，时间复杂度成指数O(n^2)上升，而且，我们在输出的时候也是需要使用for循环来实现，也是一个指数级别的复杂度实现，而且，在我们求区间的时候，其实发生了大量的重复便利，比如说我一个5元素的数组1 2 3 4 5，我需要分别求区间1~4和2~5的总和，我们直接实现的话会重复计算2~4这个区间的内容，属于一种计算的浪费。

       所以才超时了。

       那么有什么办法能够解决呢？这就要请出我们的差分数组了。

1.差分数组的定义：

对于已知有n个元素的离线数列d，我们可以建立记录它每项与前一项差值的差分数组f：显然，f[1]=d[1]-0=d[1];对于整数i∈[2,n]，我们让f[i]=d[i]-d[i-1]。

2.简单性质：

(1)计算数列各项的值：观察d[2]=f[1]+f[2]=d[1]+d[2]-d[1]=d[2]可知，数列第i项的值是可以用差分数组的前i项的和计算的，即d[i]=f[i]的前缀和。
(2)计算数列每一项的前缀和：第i项的前缀和即为数列前i项的和，那么推导可知

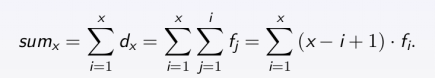
即可用差分数组求出数列前缀和；

3.用途：

(1)快速处理区间加减操作：

假如现在对数列中区间[L,R]上的数加上x，我们通过性质(1)知道，第一个受影响的差分数组中的元素为f[L],即令f[L]+=x，那么后面数列元素在计算过程中都会加上x；最后一个受影响的差分数组中的元素为f[R],所以令f[R+1]-=x，即可保证不会影响到R以后数列元素的计算。这样我们不必对区间内每一个数进行处理，只需处理两个差分后的数即可；

(2)询问区间和问题：

由性质(2)我们可以计算出数列各项的前缀和数组sum各项的值；那么显然，区间[L,R]的和即为ans=sum[R]-sum[L-1];

来自博客https://www.cnblogs.com/COLIN-LIGHTNING/p/8436624.html

简单说起来就是利用两个数组做中间值和一个求和数组（一共三个数组），来实现时间复杂度的降低，基本原理如上，在这里，我使用三个数组d[n],f[n],sum[n];三个数组均从下标记1开始，且首元素均相同，当然，它们下标为[0]的空间也不会浪费，均为0。

       首先声明1<i<=n;然后有

       d[i]=a[i]-a[i-1]

       f[i]=f[i-1]+d[i]

       sum[i]=sum[i-1]+f[i]

       通过这样的递推式即可得到一个sum数组，届时，如果我们需要求一个区间L,R的总和，只需要sum[L]-sum[R]，两个值相减即可，可以完完全全的省略掉for的递归过程，复杂度从O(N^2)降低到了O(n)的水平。

       同时如果我们需要进行区间修改的话，只需要在d[i]=a[i]-a[i-1]这一个步骤中添加，d[L]+=w,d[R+1]-=w;两步即可，同样的可以省去for循环。

       话不多说直接上代码。

#include<bits/stdc++.h>
using namespace std;
const int Max=10000;	//定义数组上限元素 
int a[Max],d[Max],f[Max],sum[Max];
int main() {
	memset(a,0,sizeof(a));
	memset(d,0,sizeof(d));
	memset(f,0,sizeof(f));
	memset(sum,0,sizeof(sum));
	//清空数组，同时也保证a[0]=d[0]=f[0]=sum[0]
	//在输入的时候从1开始保证a[1]=d[1]=f[1]=sum[1]
	int n;
	cin>>n;
	for(int i=1; i<=n; i++) {
		cin>>a[i];			//
		d[i]=a[i]-a[i-1];
	}

	int t;
	cin>>t;
	while(t--) {
		int left,right,plus;	//left表示左区间，right表示右区间，plus表示所加的值 
		cin>>left>>right>>plus;
		d[left]+=plus;
		d[right+1]-=plus;
	}

	for(int i=1; i<=n; i++) {
		f[i]=f[i-1]+d[i];
		sum[i]=sum[i-1]+f[i];
	}

	cin>>t;
	while(t--) {
		int left,right;
		cin>>left>>right;
		cout<<sum[right]-sum[left-1]<<endl;
	}
	return 0;
}

验证一下，结果正确

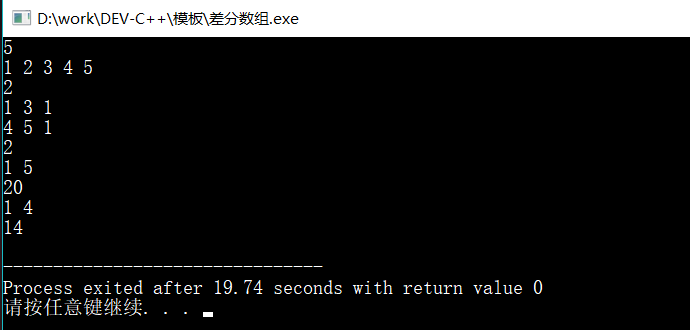
如果我们想要查看一下数组中发生了什么，可以直接把这个代码加进去

	for(int i=0;i<=n;i++){    //测试用
		printf("a[%d]\td[%d]\tf[%d]\tsum[%d]\n",i,i,i,i);
		//cout<<"a[i]\td[i]\tf[i]\tsum[i]"<<endl;
		cout<<a[i]<<'\t'<<d[i]<<'\t'<<f[i]<<'\t'<<sum[i]<<endl;
	}

以n=5的数组1，2，3，4，5为例，我们看看数组里面发生了什么

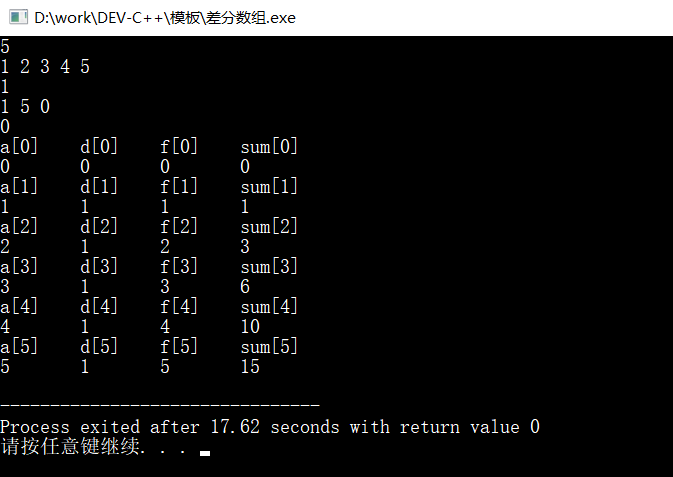
这样可以更加直白的看懂这几个中间数组到底干了什么。

以上，就是差分数组的使用了，差分数组适用于我上面讲的那种题型，但是有一个缺点就是空间复杂度相应的要比只使用一个数组的要高一些（也不会高到哪里去）。