蓝桥杯2024年第十五届省赛真题-小球反弹

先看题目：

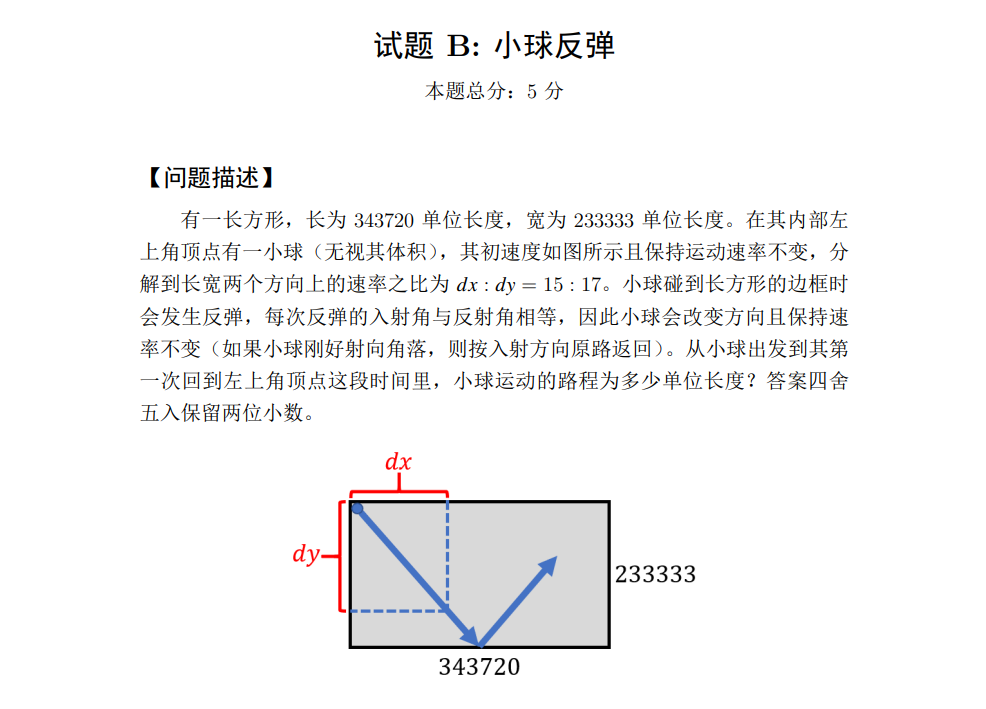
这道题目不要思考入射角反射角问题，不然题目就很麻烦了。

把小球想象出两个小球的投影 分别在x轴和y轴做往返运动，当小球在x轴往返两次（或偶数倍）同时y轴也往返了偶数倍，此时小球重回左上角顶点。

如图：

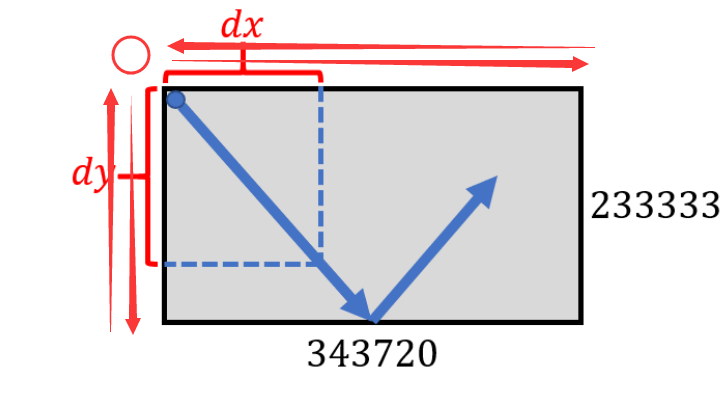
当然这题考察的是走过的路径 因为是分解到x y轴 最后的合并一定符合三角公式 c^2=a^2+b^2 即s=sqrt(sx^2+sy^2)

如图：

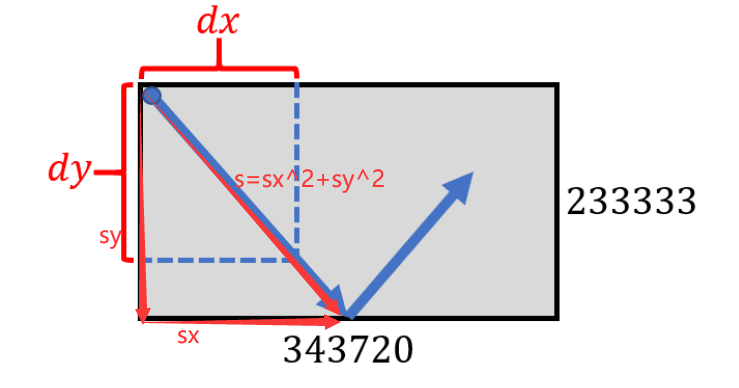
OK 条件已经知道了 现在只需要知道sx 和 sy的值即可。

设小球每秒在x轴走15米 y轴走17米 t代表秒

当15t是343720的倍数 且 17t是233333的倍数时 小球必在顶点位置。

当15t是343720的偶数倍 且 17t是233333的偶数倍时 小球在左上角顶点。

sx=15t   sy=17t

s=sqrt(sx^2+sy^2)=sqrt(15*15*t^2+17*17*t^2)=sqrt(514）* t

公式化简以后就很明了了 现在找到这个t就可以了。

代码如下：

#include <bits/stdc++.h>
using namespace std;

int main() {

	long long t=1,z;
	while(1) {
		// 是倍数 
		if(t*15%343720==0 && t*17%233333==0) {
			cout<<"t*15/343720="<<t*15/343720<<endl;
			cout<<"t*17/233333="<<t*17/233333<<endl;
			cout<<"t="<<t<<endl;
			// 且是偶数倍 
			if(t*15/343720%2==0&&t*17/233333%2==0) {
				double s = sqrt(15*15+17*17)*t;
				cout<<"s=sqrt(15*15+17*17)*t=";
				printf("%lf",s); 
				break;
			}else{
				cout<<"不是偶数倍"<<endl; 
			} 
		}
		t++;
	}

	return 0;
}

运行结果：

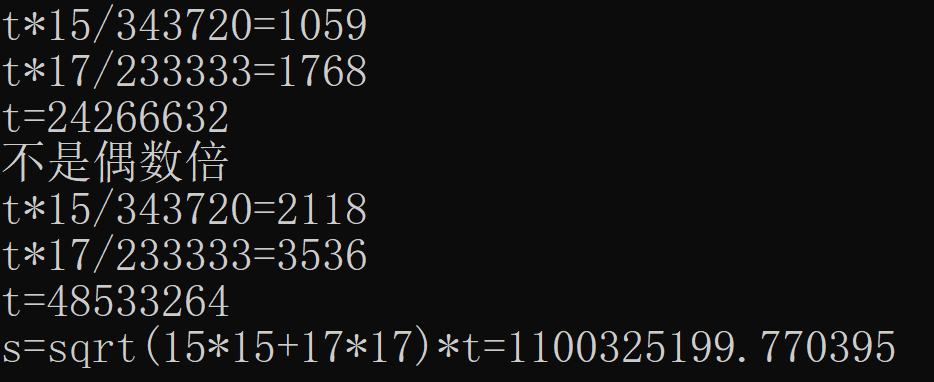
答案：1100325199.77