积木画---详细解释

解题思路:

先找到一个n的独立整体数目(n为整体表示无法从前面的n-1个当中去凑出2xn) 

当n=1时有一个整体(I型)n=2时有一个整体(横放的上下两个I型，竖直放的两个I型是n=1的独立整体拼出来的，所以不算) 

n=3时有两个：

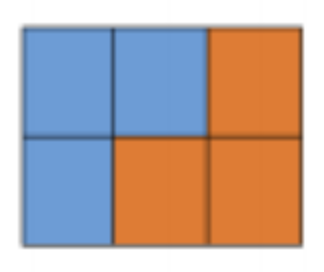
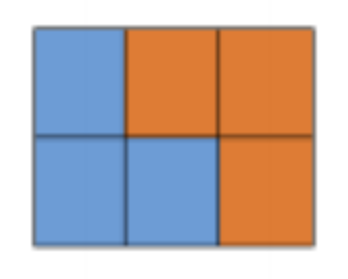
n=4时：

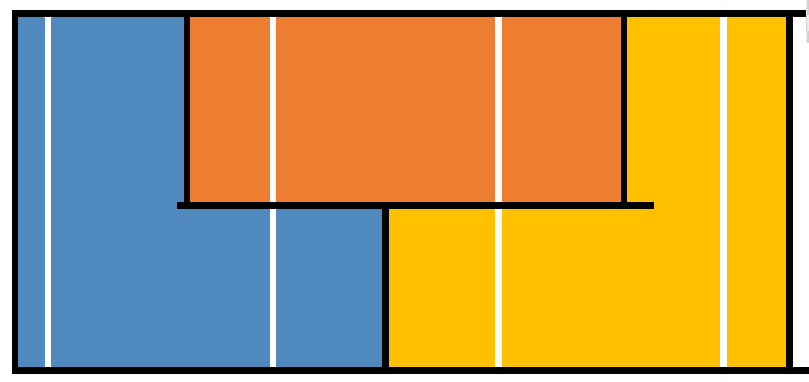
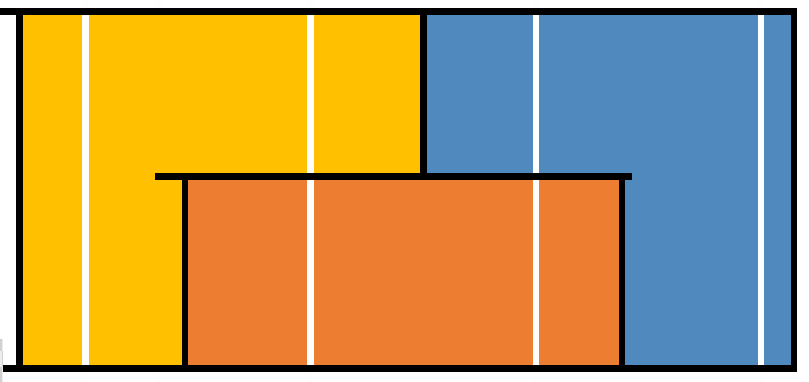
n=5 时：

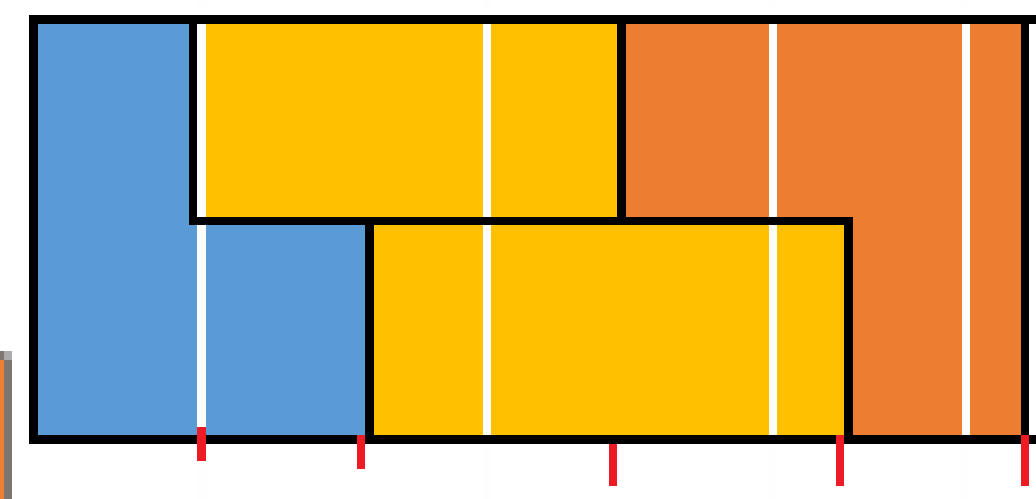
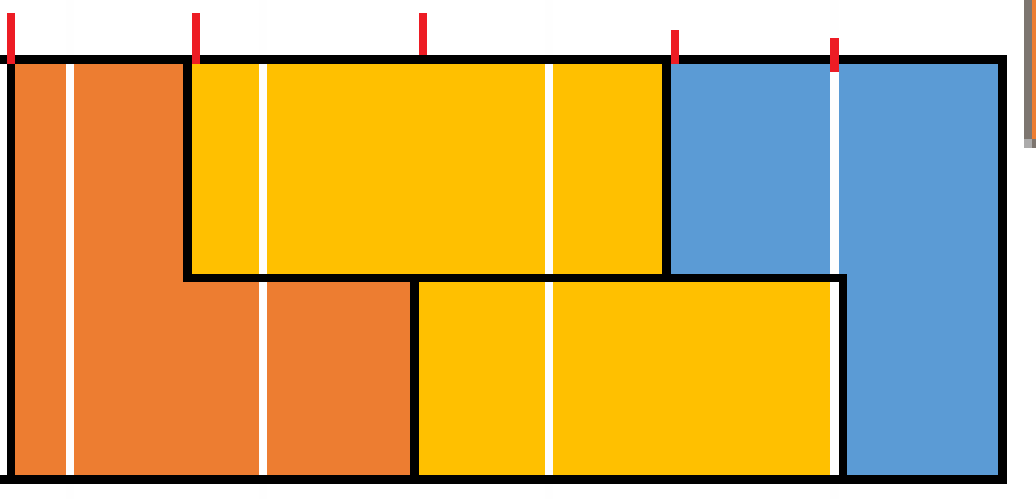
同理当n=6 ，7 ......时同样有两个 

则有：

F[n] =  F[n-1] + F[n-2] + F[n-3]*2 + F[n-4]*2 + ... 

F[n-1] = F[n-2] + F[n-3] + F[n-4]*2 + F[n-5]*2 + ...

两式相减有：

F[n] - F[n-1] = F[n-1] + F[n-3] 

即F[n] = 2 * F[n-1] + F[n-3]

参考代码:

using namespace std;
typedef long long ll;
const ll mod = 1000000007;
int main(){
//a,b,c初始为n=1 2 3的总方案数，ans记录下一个n值对应的答案 
//即F[n] = ans,F[n-1] = c,F[n-2] = b,F[n-3] = a; 
ll a = 1,b = 1,c = 2,ans;
int n;
cin>>n;
for(int i = 3;i <= n;i++){
ans = (2 * c + a) % mod;
a = b;b = c;c = ans;
}
cout<<ans;
return 0;
}