蓝桥杯算法训练VIP-传球游戏-题解（c++代码）（dfs + 剪枝）

解题思路:

由于每次传递都只能向左右传递一个单位，所以我们可以根据此特性画出下图所示二叉树（从0开始传递，一共3人传递3次）。接下来我们可以用dfs找出值为0的叶子结点数（即为球传递回0的次数），最后再用剪枝优化代码，即可AC

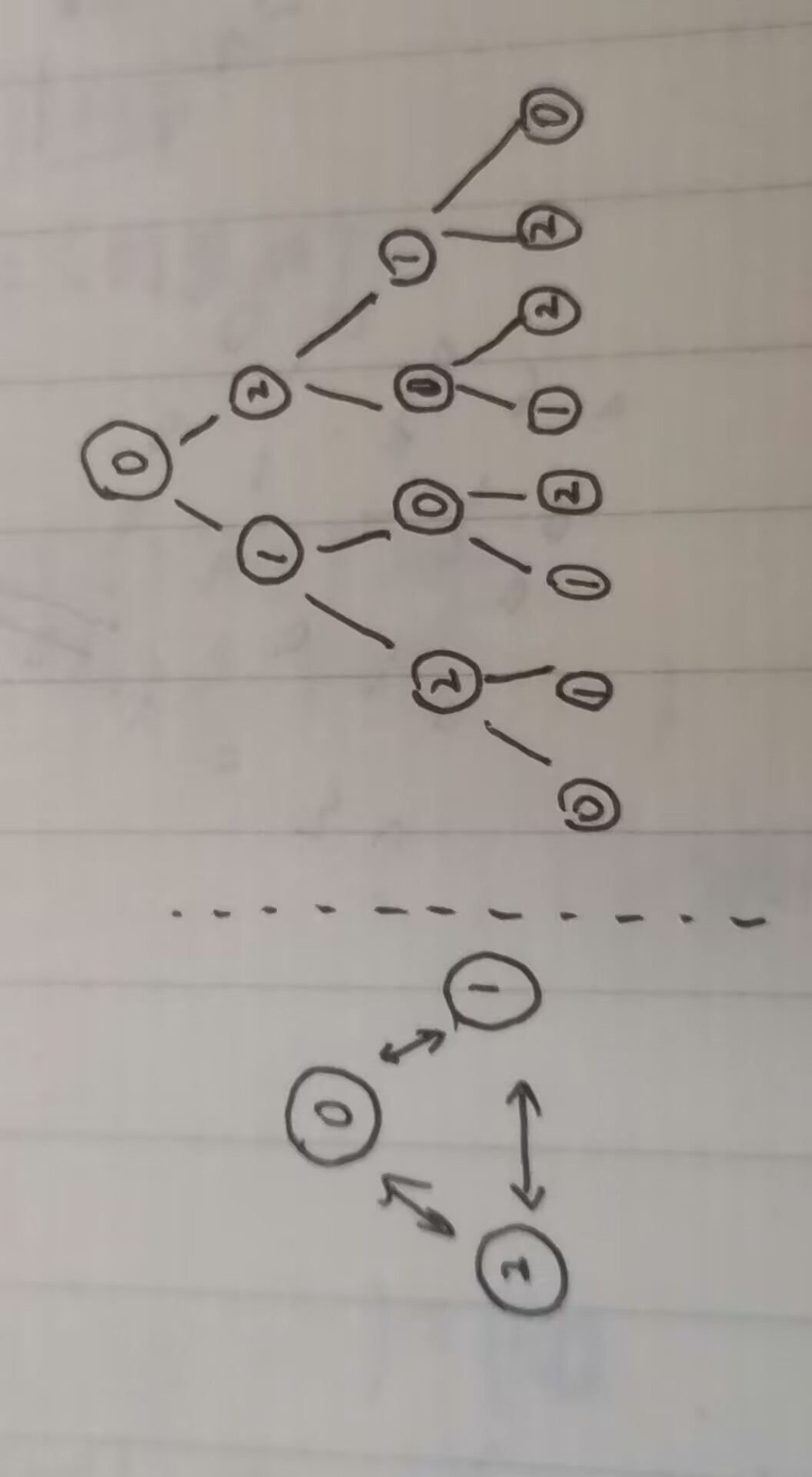
注意事项:

参考代码:

#include <bits/stdc++.h>
using namespace std;

// 定义全局变量 m 和 n，分别代表问题中的两个维度参数
int m, n;

// 初始化一个二维 vector，用于存储已经计算过的结果（记忆化）
vector<vector<int>> memo;

// 定义 dfs 函数，输入参数为当前的深度 dep 和状态 cur
int dfs(int dep, int cur) {
    // 判断当前深度和状态下的结果是否已经计算过并存储在 memo 中
    if (memo[dep][cur] != -1) {
        // 如果已计算过，则直接返回 memo 中存储的结果，避免重复计算
        return memo[dep][cur];
    }

    // 当达到最大深度时（dep == n），根据条件判断并返回最终结果
    if (dep == n) {
        if (cur == 0) {
            // 若 cur 等于 0，则返回 1，并将结果存入 memo
            return memo[dep][cur] = 1;
        } else {
            // 否则返回 0，并将结果存入 memo
            return memo[dep][cur] = 0;
        }
    }

    // 对未到达最大深度的情况，进行递归计算下一个状态的结果
    // 这里状态转移规则是：(cur + 1) % m 和 cur == 0 ? m - 1 : cur - 1
    // 并将两次递归计算的结果相加作为当前状态的结果
    return memo[dep][cur] = dfs(dep + 1, (cur + 1) % m) + dfs(dep + 1, cur == 0 ? m - 1 : cur - 1);
}

int main() {
    // 从标准输入读取 m 和 n 的值
    cin >> m >> n;

    // 初始化 memo，大小为 (n+1) x m，所有元素初始化为 -1 表示未计算过
    memo.resize(n + 1, vector<int>(m, -1));

    // 以初始深度 dep=0 和状态 cur=0 调用 dfs 函数，并输出结果
    cout << dfs(0, 0) << endl;

    // 主函数返回 0，表示程序正常结束
    return 0;
}