动态规划入门：深搜（递归）→记忆化搜索→递推（DP）

解题思路:

对于每家店，有选和不选两种选择

那选还是不选取决于我当前是否能取得最大价值

第一步:画搜索树

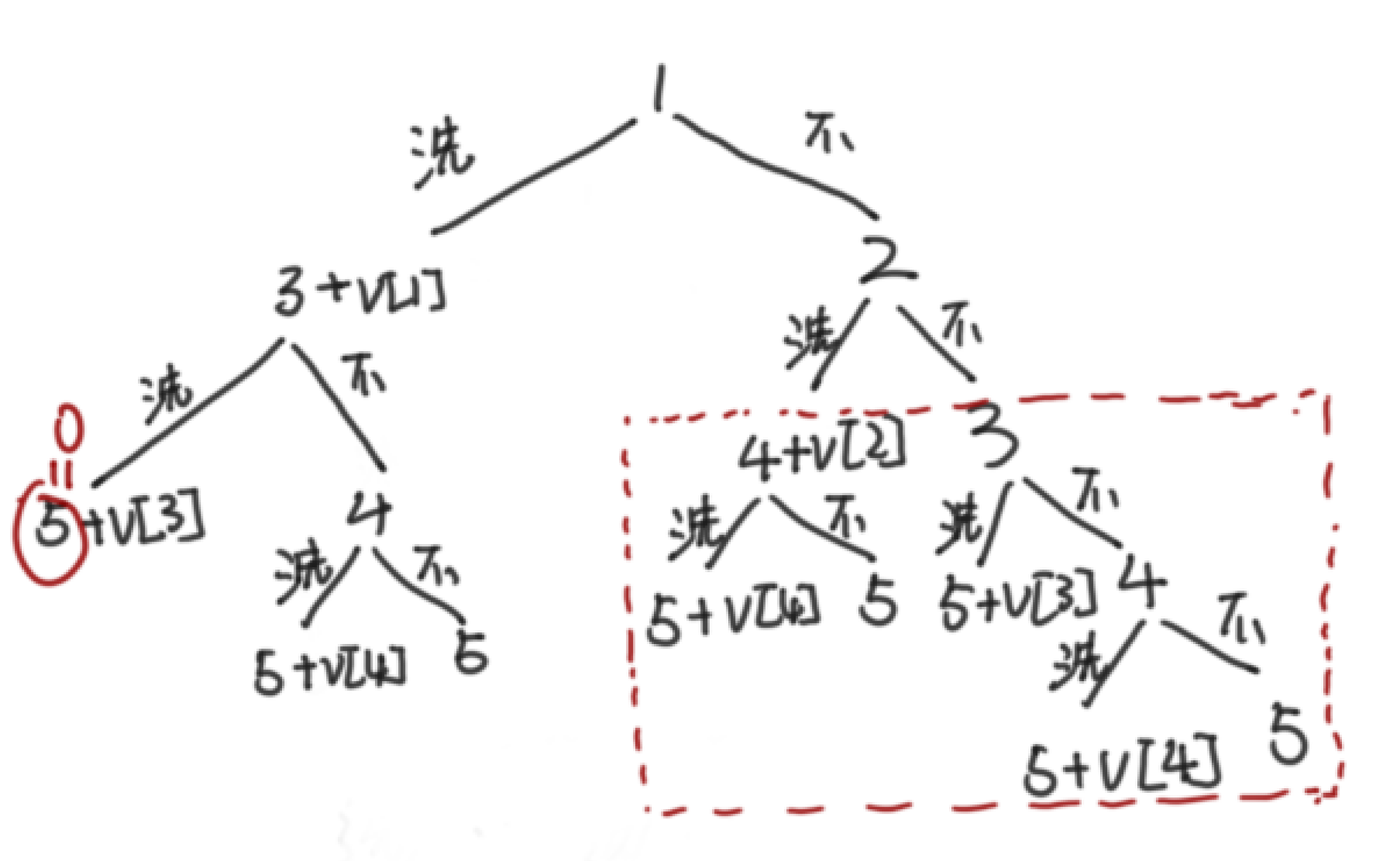
第二步：暴力DFS

关键：找到递归边界值和递归公式

递归公式:dfs(n)=max(dfs(n+1),dfs(n+2)+v[n])

递归边界：dfs(n+1)=dfs(n+2)=0

参考代码：

import java.io.*;
public class Main {
    static BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
    static PrintWriter pw=new PrintWriter(new OutputStreamWriter(System.out));
    static int shop;
    static long values[];
    public static void main(String[] args) throws IOException {
        int test=Integer.parseInt(br.readLine());
        while(test>0) {
            shop = Integer.parseInt(br.readLine());
            values = new long[shop + 1];
            String[] s = br.readLine().split(" ");
            for (int i = 1; i shop) {
            return 0;//递归的底
        }
         return Math.max(dfs(n+1),dfs(n+2)+values[n]);
    }
}

运行结果：超时

那肯定得优化

由搜索树发现，红色框内的店铺不需要继续深搜，因为在左支中已经搜过了

第三步：记忆化搜索

关键：记录之前搜索店铺i的结果

用map[x]记录从1到x店铺的最大价值sum，若map[x]!=0，返回map[x]

参考代码：

import java.io.*;
 
public class Main {
    static BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
    static PrintWriter pw=new PrintWriter(new OutputStreamWriter(System.out));
    static int shop;
    static long[]map;
    static long values[];
    public static void main(String[] args) throws IOException {
        int test=Integer.parseInt(br.readLine());
        while(test>0) {
            shop = Integer.parseInt(br.readLine());
            values = new long[shop + 1];
             map= new long[3 + shop];
            String[] s = br.readLine().split(" ");
            for (int i = 1; i shop) {
            sum=0;
        }else{
            sum=Math.max(dfs(n+1),dfs(n+2)+values[n]);
        }
        map[n]=sum;
        return sum;
    }
}

运行结果：运行错误

代码没问题，其他平台能跑

第四步：递推

关键：找到递推公式，由小推到大

递推公式：dp[i]=max(dp[i-1],dp[i-2]+values[i])

映射：因为遍历从1开始，防止下标越界，则下标偏移2

公式变成：dp[i+2]=max(dp[i+1],dp[i]+values[i])

参考代码：

import java.io.*;
 
public class Main {
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
    static int shop;
    static long values[];
    public static void main(String[] args) throws IOException {
        int test = Integer.parseInt(br.readLine());
        while (test > 0) {
            shop = Integer.parseInt(br.readLine());
            values = new long[shop + 1];
            String[] s = br.readLine().split(" ");
            for (int i = 1; i <= shop; i++) {
                values[i] = Integer.parseInt(s[i - 1]);
            }
            long []dp=new long[shop+3];//dp[i]存1-i家店洗劫后取得的最大价值
            for (int i = 1; i<=shop; i++) {
                dp[i+2]=Math.max(dp[i+1],dp[i]+values[i]);
            }
            pw.println(dp[shop+2]);
            pw.flush();
            test--;
        }
    }
}

运行结果：100分  运行时间: 1585ms    消耗内存: 50880KB

进一步优化：

因为递推公式只涉及i，i-1，i-2三个数

每次循环只需要三个值就可以得出此次循环的答案，不需要用dp数组记录每次循环的结果

用三个变量newf，tmp1，tmp2记录每次循环的结果，并在循环里更新newf，tmp1，tmp2方便下次计算

主要优化空间：数组→变量

参考代码：

import java.io.*;
 
/**
 * @Author:杨雨彤
 * @date:2024/2/18 10:00
 */
public class Main {
    static BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
    static PrintWriter pw=new PrintWriter(new OutputStreamWriter(System.out));
    static int shop;
    static long values[];
    public static void main(String[] args) throws IOException {
        int test=Integer.parseInt(br.readLine());
        while(test>0) {
            shop = Integer.parseInt(br.readLine());
            values = new long[shop + 1];
            String[] s = br.readLine().split(" ");
            for (int i = 1; i <= shop; i++) {
                values[i] = Integer.parseInt(s[i - 1]);
            }
            long newf = 0, temp1 = 0, temp2 = 0;
            for (int i = 1; i <= shop; i++) {
                newf = Math.max(temp1, temp2 + values[i]);
                temp2 = temp1;
                temp1 = newf;
            }
            pw.println(newf);
            pw.flush();
            test --;
        }
    }
 
}

运行结果：100分 运行时间: 1858ms    消耗内存: 46252KB

最后：这道题是跟着B站上一位up主写的。

每次想学dp都无所适从，到底从哪开始呢？状态转移方程怎么推出来的？

在无数次探索中终于找到了答案

那就是暴力DFS→记忆化搜索→递推（DP）

动态规划也分很多种，线性，树形..但没关系只要找到门还怕什么！！

最后的最后：

其实我一开始的思路不是这样的，对每个店铺都有选和不选

套用01背包的思想,店铺dp[i][0]表示第i家店不偷时，洗劫前i家店铺所能取的最大价值

dp[i][1]表示第i家店偷时，洗劫前i家店能取得的最大价值

最后的答案就在,dp[n][0]和dp[n][1]中取较大的

对于dp[i][0]递推公式为：dp[i][0]=max(dp[i-1][1],dp[i-1][0])

理解：如果第i家店不偷，那么第i-1家店偷不偷都可以，最后取决于dp[i-1][0]和dp[i-1][1]谁大

对于dp[i][1]递推公式为：dp[i][1]=max(dp[i-1][0],dp[i-2][1])

理解：如果第i家店偷，要么第i-1家店不能偷，要么第i-2家店被偷，从而只能偷i了

注意事项:

dp[i][1]既然偷了第i家店，那么dp[i][1]初始值就是该店铺的价值values[i]

递推的边界：dp[1][0]=0,dp[1][1]=values[1];

参考代码:

import java.beans.Visibility;
import java.io.*;
 
/**
 * @Author:杨雨彤
 * @date:2024/2/18 10:00
 */
public class Main {
    static BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
    static PrintWriter pw=new PrintWriter(new OutputStreamWriter(System.out));
    static int shop;
    static long values[];
    public static void main(String[] args) throws IOException {
        int test=Integer.parseInt(br.readLine());
        while(test>0) {
            shop = Integer.parseInt(br.readLine());
            values = new long[shop + 1];
            String[] s = br.readLine().split(" ");
            for (int i = 1; i <= shop; i++) {
                values[i] = Integer.parseInt(s[i - 1]);
            }
        long [][]dp=new long[shop+1][2];//dp[i][0]表示第i家商店不偷时，前i个店铺的最大价值
            //dp[i][1]表示第i家店偷时，前i家店铺的最大价值，初始值就是第i家店铺偷时所取得的价值
        dp[1][0]=0;//第1家店不偷
        for (int i = 1; i <=shop ; i++) {
            dp[i][1]=values[i];
        }
        for (int i = 2; i <=shop ; i++) {
           dp[i][0]+=Math.max(dp[i-1][0],dp[i-1][1]);
           dp[i][1]+=Math.max(dp[i-1][0],dp[i-2][1]);
        }
        pw.println(Math.max(dp[shop][0],dp[shop][1]));
        pw.flush();
            test --;
        }
    }
}

运行结果：100分 运行时间: 1714ms    消耗内存: 52512KB