2659: 蓝桥杯2022年第十三届省赛真题-统计子矩阵

解题思路:

二维前缀和然后循环判断当前区间是否符合小于等于K

这样就需要指定两个点，每一个点有x,y方向坐标，这样就是4重循环，4个for会有三个点超时，代码如下

#include<iostream>

using namespace std;

const int N=1000;

int dp[N][N];

int a[N][N];

int n,m,k1;

int ans;

int main(){

cin>>n>>m>>k1;

for(int i=1;i<=n;i++){

for(int j=1;j<=m;j++) {

cin>>a[i][j];

dp[i][j]=dp[i][j-1]+dp[i-1][j]-dp[i-1][j-1]+a[i][j];

}

}

for(int i=1;i<=n;i++){

for(int j=1;j<=m;j++){

for(int k=i;k<=n;k++){

for(int l=j;l<=m;l++){

if((dp[k][l]-dp[i-1][l]-dp[k][j-1]+dp[i-1][j-1])<=k1) ans++;

// cout<<ans;

}

}

}

}

cout<<ans;

return 0;

}

正解是一维前缀和加双指针，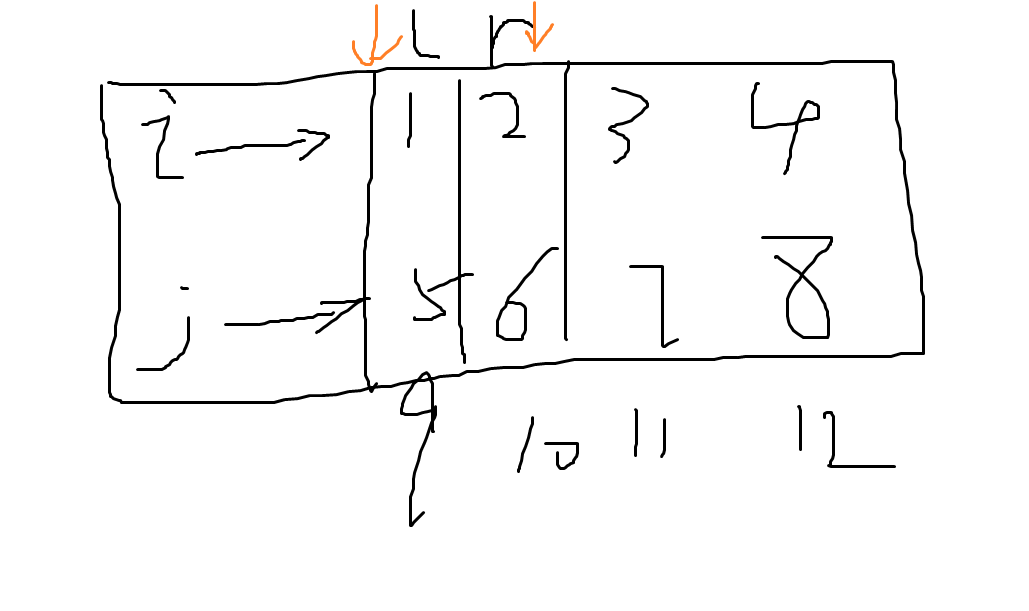

i,j控制上下，l,r控制左右，时间复杂度来到n^3

代码如下：

#include<iostream>

using namespace std;

const int N=510;

int n,m,k;

int a[N][N];

int dp[N][N];

long long ans;

int main(){

cin>>n>>m>>k;

for(int i=1;i<=n;i++){

for(int j=1;j<=m;j++){

cin>>a[i][j];

dp[i][j]+=dp[i-1][j]+a[i][j];

}

}

for(int i=1;i<=n;i++){

for(int j=i;j<=n;j++){

for(int l=1,r=1,sum=0;r<=m;r++){

sum+=dp[j][r]-dp[i-1][r];

while(sum>k){

sum-=dp[j][l]-dp[i-1][l];

l++;

}

ans+=r-l+1;

}

}

}

cout<<ans;

}

注意事项:
看一下总数ans,会不会超int