《数组排序》续集——既万能，又难写的快速排序

我在之前写过一篇关于数组排序的四种方法的文章（未看过的朋友可以翻一下前面的文章，叫做《数组排序的四种方法》），对于广大的编程学生来说，这些足矣。但是这些排序各有各的缺点（选择排序除外），于是，今天我来说一下还算全面的排序方法——快速排序！

咱们先来扒一扒之前三种排序的缺点（选择排序除外）：

1. 选择排序
   

这个排序其实还是比较快的，也比较好写，时间复杂度也行，可以说是快速排序外最好的方法，也是我比较认同的排序

2.冒泡排序

这个排序写起来很简单，但是——他的时间复杂度贼高！而且极不稳定。情况好，速度快；情况坏，速度慢（复杂度O(N的平方)）

3.sort排序

这个是自带的函数，还不错，但是缺乏多样性。比如我只要排序前面三个，或者按规定排序，这就很尴尬（他给你全部从小到大排好了）

好的，言归正传，接下来就是本场的主角——快速排序

注：本章难道极高，可以跳过不看

首先讲一下算法：

（这里借用一下啊哈磊的文章）

先找一个基准数（默认为这组数的第一个）

例：6 1 2 7 9 3 4 5 10 8，这里的基准数为6（其实就是参照数，别被吓到了）

(这里要用数组）

我们建立两个变量，分布记录最右及最左的数，就叫他们“哨兵i”和“哨兵j”

好的，现在哨兵j出动，从右向左移动（j--）（这里的i，j中所含的数是数组的下标）

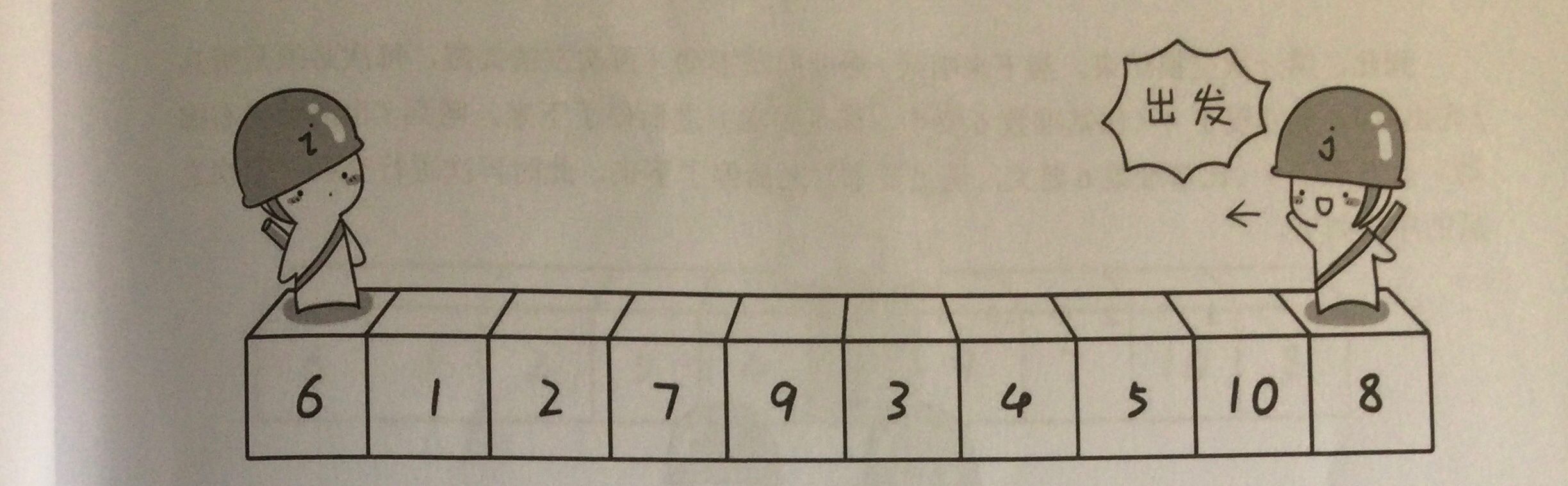
每次一定是哨兵j先出动，这非常重要。

哨兵j先向前移动，直到碰见比基准数小的数。

好的，现在哨兵j停在了5上，说明此时的数(a[j])是小于基准数6的

接着让哨兵i出发，直到碰见比基准数大的数

好的，此时哨兵i停在了7上面，说明此时的数(a[i])是大于基准数6的

这时候我们将它们交换：

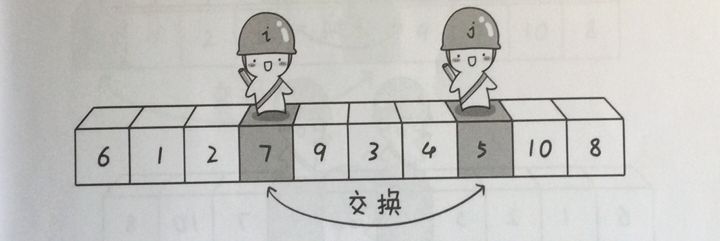
交换后就成了这样：

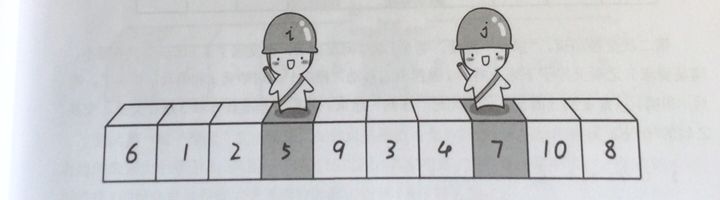
交换之后的序列如下：

6 1 2 5 9 3 4 7 10

接下来一直重复这个动作，直到哨兵i和哨兵j相遇，即都找到了一个数上：

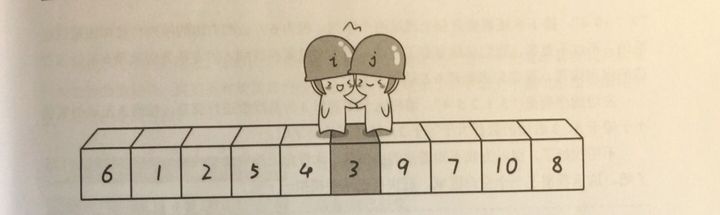
这说明第一轮“探测”结束了，将这个数与基准数交换：

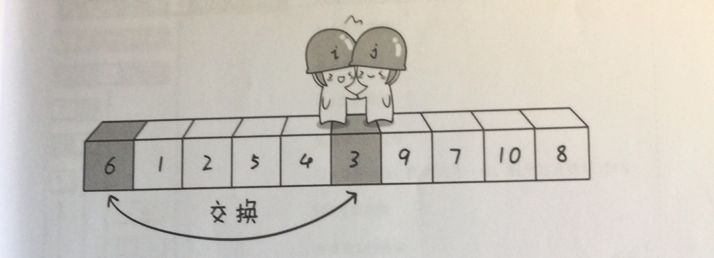
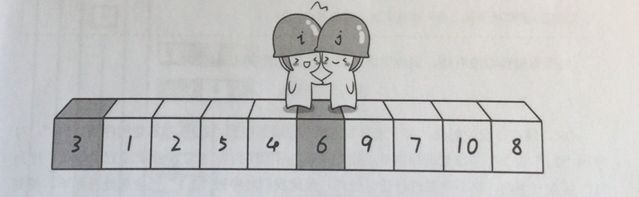
此时第一轮“探测”结束，我们可以发现：6右边的数都是大于6的数，6左边的数都是小于6的数

“6”把整个数列分割成了两段

此时我们要同时排列两个数列，一个是从最左边(a[1])到中间前一个位置（a[i-1])的，一个是中间后一个位置的(a[i+1])到n

这是一个递归的过程（quicklysort(left,i-1);quicklysort(i+1,right))

其实，快速排序就是将每一轮的基准数归位，当所有基准数都归位时，排序也就结束了

接下来上个霸气的图：

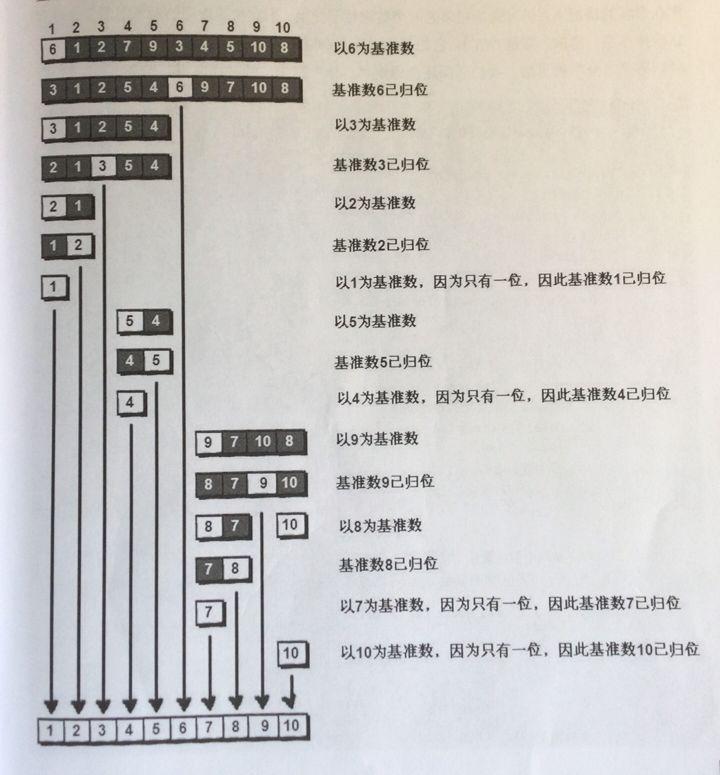
代码如下：

#include<bits/stdc++.h>
using namespace std;
int a[1000],n;
void quick(int left,int right)
{
    int i,j,temp,shu;
    if(left>right)
    {
        return;
    }
    temp=a[left];
    i=left;
    j=right;
    while(i!=j)
    {
        while(a[j]>=temp&&i<j)
        {
            j--;
        }
        while(a[i]<=temp&&i<j)
        {
            i++;
        }
        if(i<j)
        {
            shu=a[i];
            a[i]=a[j];
            a[j]=shu;
        }
    }
    a[left]=a[i];
    a[i]=temp;
    quick(left,i-1);
    quick(i+1,right);
    return;
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
    }
    quick(1,n);
    for(int i=1;i<=n;i++)
    {
        cout<<a[i]<<" ";
    }


    return 0;
}

现在来说一下为什么快速排序快——

虽然相较于冒泡排序，都是交换，但是每次交换都是跳跃性的，不像冒泡排序一样只能交换相邻的两个数。

因此比较和交换的次数少得多

但其实他也不是万能的，在最差的情况下跟冒泡排序一样，都是交换相邻的两个数。

而且不稳定。

而且最最重要的是——太难写了！！！

本次就教到这里了，制作不易，给个高分，谢谢！