python-8皇后·改

解题思路:

首先解释一下8皇后这个问题。

在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

思路：

①创建一个组1*8的数组A[],其中A[i]代表第i行第A[i]列的值。创建一个递归函数queen(A,cur = 0)，参数A即为8*1的矩阵，参数cur为行数。递归的出口为行数等于8时，返回。

例如，解释一下8皇后一个成功摆放的案例。A = [0, 4, 7, 5, 2, 6, 1, 3]

第0行第0个位置可以摆放

第2行第4个位置可以摆放

第3行第7个位置可以摆放

......

第7行第3个位置可以摆放。

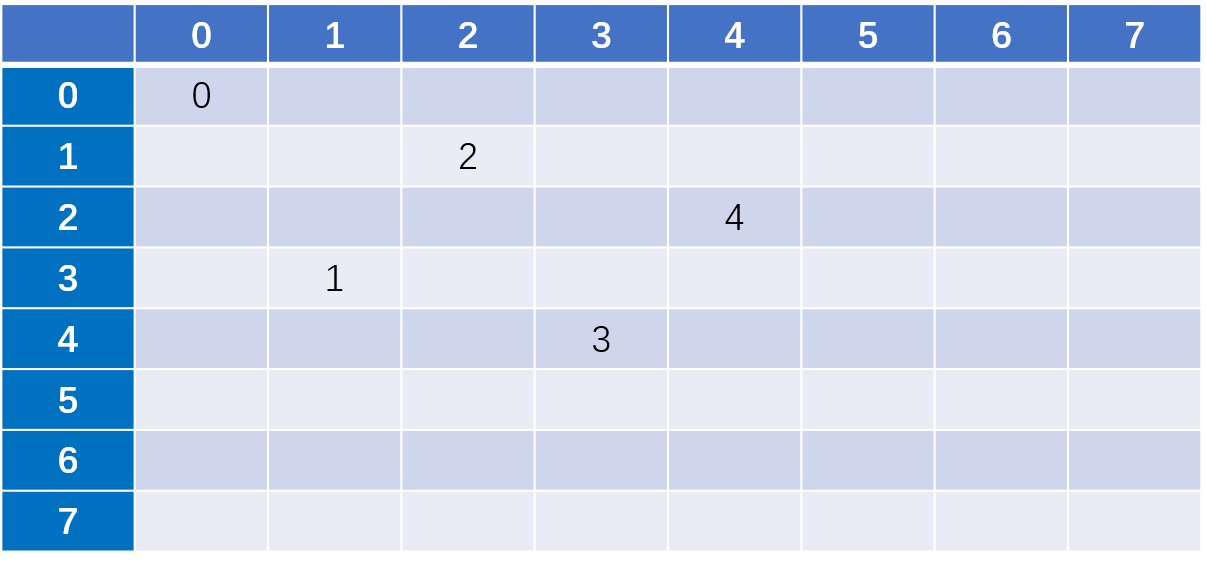
接下来以下图解释一下递归的过程

对每一行进行遍历，把第j列的值赋给A[i]，判断一下是否冲突，如果不冲突，继续递归，如果冲突，则遍历该行的下一列。

开始第0行第0列可以摆放，那么A[0] = 0,

接下来第1行中，第0列与第0行在同一列，冲突，第1列与第0行在一条斜线上，冲突，第2列不冲突，可以摆放。A[1] = 2

接下来第2行中，第0列与第0行在同一列，冲突，第1列与第1行在一条斜线上，冲突，第2列与第1行在同一列，冲突，第3列与第1行在一条斜线上，冲突，第四列不冲突，可以摆放。A[2] = 4

......

按照这种规律往下进行，我们发现，当扫面第5行时，每一列都会与之前的行冲突。因此，这种排放情况是行不通的。

按照这种规律遍历结束，我们可以得到所有8皇后的解，从中找出最大值即可。

注意事项:

参考代码:

from cmath import inf  
  
  
def queen(A,cur = 0):  
    global Matrix  
    global maxnum  
    if cur == 8:  
        sum = 0  
        for i in range(8):  
            sum = sum + Matrix[i][A[i]]  
        if sum > maxnum:  
            maxnum = sum  
        return  
      
    for j in range(8):  
        A[cur] = j  
        for i in range(cur):  
            if A[i] == j or abs(j - A[i]) == cur - i:  
                break  
        else:  
            queen(A,cur+1)  
  
  
Matrix = [[int(j) for j in input().strip().split()] for i in range(8)]  
maxnum = -inf  
queen([None]*8)  
print(maxnum)