解题思路:
首先,定义整数N;写出N从1到6的每一个数的尼科彻斯等式,观察规律;如下:
N
1^3=1 1=1^2+(1-1)
2^3=3+5 5=2^2+(2-1) 3=1+2
3^3=7+9+11 11=3^2+(3-1) 7=5+2
4^3=13+15+17+19 19=4^2+(4-1) 13=11+2
5^3=21+23+25+27+29 29=5^2+(5-1) 21=19+2
6^3=31+33+35+37+39+41 41=6^2+(6-1) 31=29+2
……………………………………
N^3= 红= (N)^2+(N-1) 蓝= (N-1)^2+((N-1)-1)+2
根据上面规律归纳总结得到:
(1)N等于N个连续奇数的和;
(2)N的尼科彻斯等式中,第一个奇数,等于N-1的尼彻尼科彻斯等式中,最后一个奇数+2;
(3)N-1的尼科彻斯等式中,最后一个奇数等于(N-1)^2+( (N-1)-1);
编程思路就是:
输入一个整数N;
求出它的尼科彻斯公式中第一个奇数
循环输出N-1个奇数和加号(在第一个基础上加上2)
输出最后一个奇数,不带加号;
注意事项:
输出“1*1*1=1=”这部分时,如:printf("%d*%d*%d=%.0lf=",N,N,N,pow(N,3));
pow返回值不是int型,故不可以用%d,并且题目输出没有小数;
题目说让验证,不止一组测试值,以文件结束符结束;
运行图:
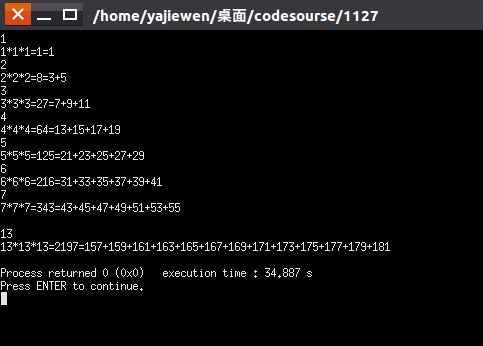
参考代码:
#include<stdio.h>
#include<math.h>
int main()
{
int N;
while(scanf("%d",&N)!=EOF)
{
int each_oddnum=pow(N-1,2)+(N-1-1)+2;
printf("%d*%d*%d=%.0lf=",N,N,N,pow(N,3));
for(int i=1;i<N;i++)
{
printf("%d+",each_oddnum);
each_oddnum+=2;
}
printf("%d\n",each_oddnum);
}
return 0;
}0.0分
27 人评分
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程

#include <stdio.h> int main() { int m,i,sum,n=1; scanf("%d",&m); while(n) { sum=0; for(i=n;i<2*m+n;i+=2) sum=sum+i; if(sum==m*m*m) { printf("%d*%d*%d=%d=",m,m,m,m*m*m); for(i=n;i<2*m+n;i+=2) { if(i==2*m+n-2) printf("%d",i); else printf("%d+",i); } break; } n+=2; } return 0; }#include<stdio.h> int main() { int sum=0,i,j,k,z; int n; scanf("%d",&n); j=n*n+(n-1)-(n-1)*2; z=n*n*n-1; k=n*n*n; printf("%d*%d*%d=%d=",n,n,n,k); for(i=1;i<=n;i++) { printf("%d",j); if(i!=n) printf("+"); j+=2; } return 0; } 我觉得我这个菜鸟版非常好理解#include<stdio.h>//请问这个错在哪,编译时没有问题啊,怎么一提交就说错 int main() { int i, j, n=13, sum, count; int result = n * n * n; for (i = 1; i <= result; i = i + 2) { count = 0; sum = 0; for (j = i; j <= result; j = j + 2) { sum += j; count++; if (count == n) break; } if (sum == result) { printf("%d*%d*%d=", n, n, n); count = 0; for (j = i; j <= result; j = j + 2) { if (count < n - 1) printf("%d+", j); else printf("%d", j); count++; if (count == n) break; } break; } } return 0; }#include<stdio.h> int main() { int n,m; scanf("%d",&n); printf("%d*",n); printf("%d*",n); printf("%d=",n); printf("%d=",n*n*n); for(m=n;m<n*n*n;m++) { if(n*n*n==m*n+n*n-n) { printf("%d",m); for(n-1;n-1>0;n--) {printf("+%d",m+2); m=m+2; } } } return 0; }#include<stdio.h> int main(void){ int a,sum,mid,i,n; printf("input something:\n"); scanf("%d",&a); sum=a*a*a; mid=a*a; i=mid-a+1; printf("%d*%d*%d=%d=%d",a,a,a,sum,i); for(n=1;n<a;n++){ printf("+%d",i+2*n); } printf("\n"); return 0; }没有用到人工计算,直接程序破解: #include <stdio.h> int main() { int n,s,i,j,x; scanf("%d",&n); for(i=1;i<=n*n*n;i=i+2){ x=0; s=0; for(j=i;x<n;j=j+2){ s=s+j; x++; } if(s==n*n*n){ printf("%d*%d*%d=%d=%d",n,n,n,n*n*n,i); x=i; for(j=1;j<n;j++){ x=x+2; printf("+%d",x); } return 0; } } } 有点麻烦。。。有没有大佬帮忙看看,我这个错误百分之17,错在哪儿 #include<stdio.h> #include<math.h> int main() { int m=0,i,j; scanf("%d",&m); for(i=1;i<m*m*m;i++) { if(m*m*m==(i+m-1)*m&&i%2==1) { printf("%d*%d*%d=%d=",m,m,m,m*m*m); for(j=i;j<i+2*m-2;j=j+2) {printf("%d+",j); } printf("%d",i+2*m-2); } } return 0; }