回文素数的快速搜寻

解题思路:偶数位的回文素数只有11，这可以让我们快速处理n是偶数的情况，证明如下

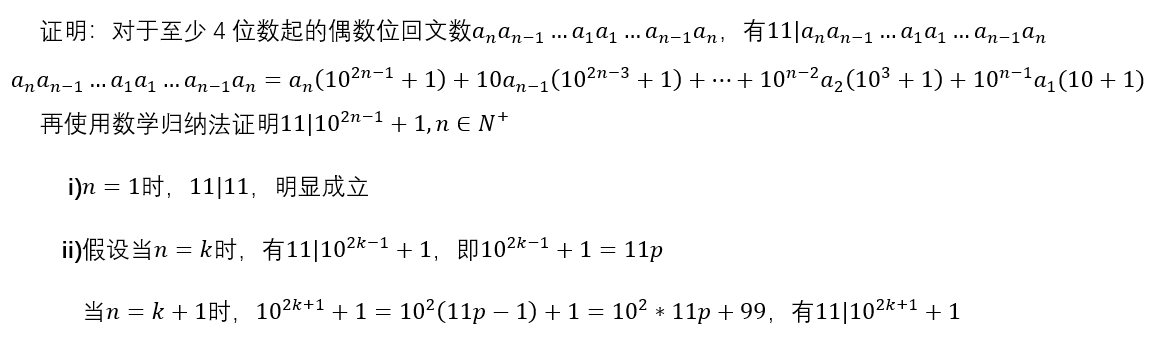
一开始我是用埃氏筛处理n是奇数的情况，但是当n=9的时候，从100000000到999999999的筛完后，再对素数判断它是否为回文数，结果超时了。循环的数字太多了！转换下思路，我们手动构造回文数，只需要从10000遍历到99999即可，然后再对每个回文数用根号方法(不用根号方法仍然会超时！)判断它是否是素数即可，动态存储结果，最后再输出就行了

参考代码:

#include<stdio.h>
#include<math.h>
#include<stdlib.h>
int f(int n)
{
	if(n==1)
		return 0;
	for(int i=2;i<=sqrt(n);i++)
		if(n%i==0)
			return 0;
	return 1;
}

int main()
{
	int n;
	scanf("%d",&n);
	if(n%2==0)
	{
		if(n==2)
			printf("1\n11");
		else
			printf("0");
	}
	else
	{
		// 构造回文数   用埃氏筛查找9位数的回文素数会超时
		// 对于n位奇数位的回文数   可以构造(n+1)/2位的数字对称生成
		int beginnum=1*pow(10,(n+1)/2-1),endnum=1*pow(10,(n+1)/2)-1;
		int *s = (int *)malloc(n*sizeof(int));
		int index,tempnum,sum=0,*allnum=NULL;
		for(int i=beginnum;i<=endnum;i++)
		{
			// 分解位数
			index=0,tempnum=i;
			while(tempnum!=0)
			{
				s[(n-1)/2+index]=s[(n-1)/2-index]=tempnum%10;
				tempnum=tempnum/10;
				index++;
			}
			if(s[0]%2==0&&n>1)
				continue;
			else
				for(int j=0;j<n;j++)
					tempnum=tempnum+s[j]*pow(10,j);
			if(f(tempnum)==1)
			{
				sum++;
				allnum = (int *)realloc(allnum,sum*sizeof(int));
				allnum[sum-1]=tempnum;
			}
		}
		// 输出结果
		printf("%d\n",sum);
		for(int i=0;i<sum;i++)
			printf("%d ",allnum[i]); 
	}
}