2086: 蓝桥杯算法提高VIP-最长公共子序列 [dp] （java代码）

 解题思路：

                    以二维数组的方式遍历两个字符串，行和列要加一，方便计算，

                       当遍历的两个字符相同时，就代表他两个字符串中都有这个字符，

                       就让这个位置等于左上角的数字加一,dp[i][j] = dp[i-1][j-1] + 1;

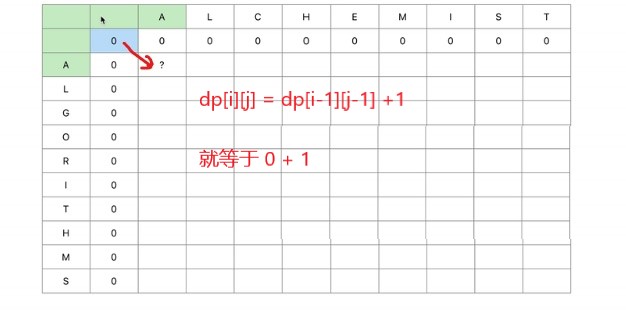
                       当两个字符不相等时，让他等于之前记录的公共串，此位置等于，

                      上面和左边两个数中大的那个数，dp[i][j] = Math.max(dp[i][j-1],dp[i-1][j]);

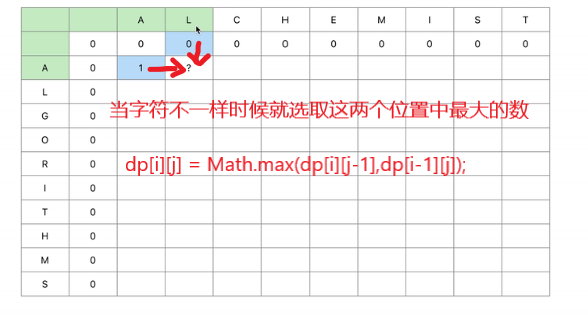
                       最后输出二维数组的最后一位就可以了。

                                根据题目样例的表格是这样的：

                                              a   b   c   d   g   h
                                         0   0   0   0   0   0   0
                                    a   0   1   1   1   1   1   1
                                    e   0   1   1   1   1   1   1
                                    d   0   1   1   1   2   2   2
                                    f    0   1   1   1   2   2   2
                                    h   0   1   1   1   2   2   3
                                    b   0   1   2   2   2   2   3

                                  // 动态转移方程式为
                                  if     ar[i] !=  ar[j]   dp[i][j] = Math.max(dp[i][j-1],dp[i-][j])
                                  else   dp[i][j] =  dp[i-1][j-1] + 1;
                                  // 在题目里面就是
                                   if (s.charAt(i-1) != t.charAt(j-1)){
                                      dp[i][j] = Math.max(dp[i][j-1],dp[i-1][j]);
                                   }else {
                                      dp[i][j] = dp[i-1][j-1] + 1;
                                   }

注意事项：

                        主要要搞懂状态转移方程式，理解了就很简单，然后代入编程里面实现就好了。

参考代码:

import java.util.Scanner;
public class Main{
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String s = sc.next();
        String t = sc.next();
        int n = s.length()+1,m = t.length()+1;
        int[][] dp = new int[n][m];
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < m; j++) {
                if (s.charAt(i-1) != t.charAt(j-1)){
                    dp[i][j] = Math.max(dp[i][j-1],dp[i-1][j]);
                }else {
                    dp[i][j] = dp[i-1][j-1] + 1;
                }
            }
        }
        System.out.println(dp[n-1][m-1]);
    }
}